Leyic
- 6
- 0
I would like to simulate the vibrations of a thin film polymer in vacuum using nonlinear analysis. For this purpose I am using an FEM program I have written in MATLAB. I do not have any data regarding damping in the structure, so I am estimating the damping using stiffness-proportional-only Caughey damping and adjusting the damping ratio until results appear reasonable. This strategy seems to be working for finding the steady-state result, but does nothing for the high frequency oscillations induced by the discretization. This is revealed in the series of figures below:
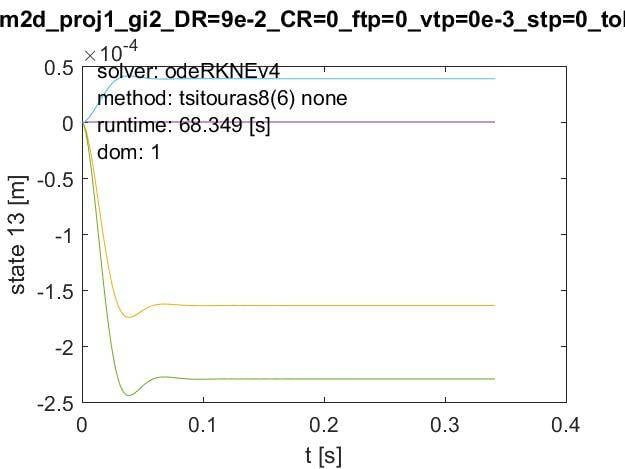
The above plots appears reasonable, but upon zooming in on the lower plot:
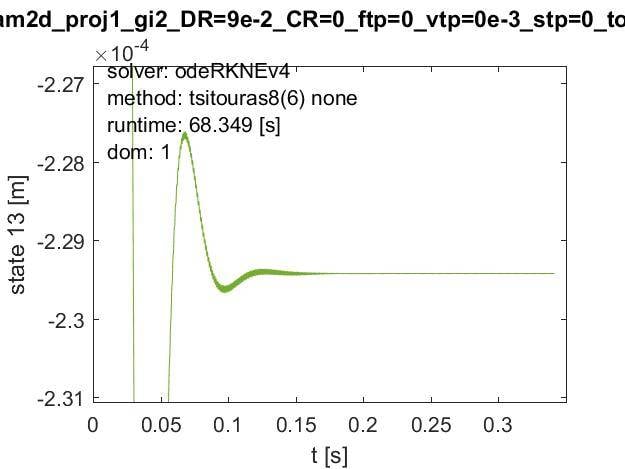
a high frequency, low amplitude oscillation is revealed. Zooming in further:
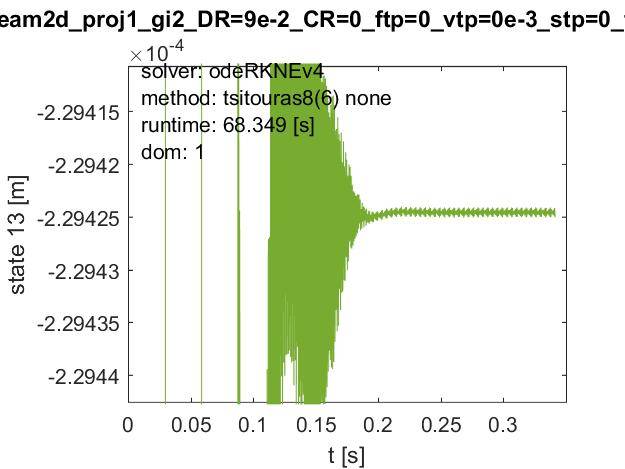
shows that this oscillation is not damped out, but persists at a non-relevant scale. This causes the simulation to run slow even after steady-state should have been achieved.
I have made one attempt to work around the issue by introducing artificial static friction to cause nodes to stick when near steady-state, but this only induces the oscillations to grow (thought to be due to compounding forces from neighboring non-stuck nodes).
Is there some other approach I could take to damp the high frequency oscillations? A non-exhaustive search of academic literature via Google only turned up results on Rayleigh damping and elementary viscoelastic models. If there is some terminology specific to this particular problem, I am not aware of it.
The above plots appears reasonable, but upon zooming in on the lower plot:
a high frequency, low amplitude oscillation is revealed. Zooming in further:
shows that this oscillation is not damped out, but persists at a non-relevant scale. This causes the simulation to run slow even after steady-state should have been achieved.
I have made one attempt to work around the issue by introducing artificial static friction to cause nodes to stick when near steady-state, but this only induces the oscillations to grow (thought to be due to compounding forces from neighboring non-stuck nodes).
Is there some other approach I could take to damp the high frequency oscillations? A non-exhaustive search of academic literature via Google only turned up results on Rayleigh damping and elementary viscoelastic models. If there is some terminology specific to this particular problem, I am not aware of it.