- #1
jeisson botache
- 4
- 1
Hi, i am an student of civil engineering and i am doing my graduate thesis. so sorry if i misspell, english is not my native languaje. so, here we go :D
Before entering in details you (whoever you are) most know:
The system is scaled for obvious reasons. The system consists of a wood board (thickness=2", mass=17.34kg) which is over a seismic test table in laboratory. Between table and wood are the important things:
*steel spheres: support the weigh of the system vertically, rails under and over (seismic table shakes in one direction).
*restoring magnets: there is 3 magnets adhered to the seismic table and 4 adhered to the system. they are placed in patter to repulsive one with the other. this is made to restore the system to it's "zero"
*damping magnet: 3 (but united as 1) magnets are adhered in the system, an aluminium plate is placed below it and adhered to the seismic table. this will create eddy brakes and will "stop" the system from keep moving in the time.
(you will know what i am talking about in equations section)
The steel spheres most spin as the seismic table shakes, but, they have a rolling resistance. the transmissibility will be higher if the rolling resistance is it too. horizontal test throw a rolling resistance of fr=0.3N
As the magnetic force increases as the magnets are close between them, i did an force vs displacement static test, this is the result:
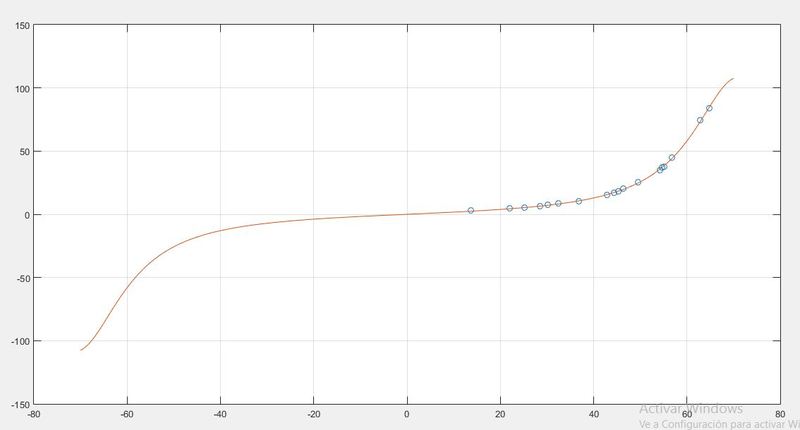
(result of horizontal test, load(N) vs relative displacement(mm))
dots means this is one direction test u+, as magnets are placed symmetrically u- is supossed to be equally.
So, in here starts da big deal: here is the system diagram:
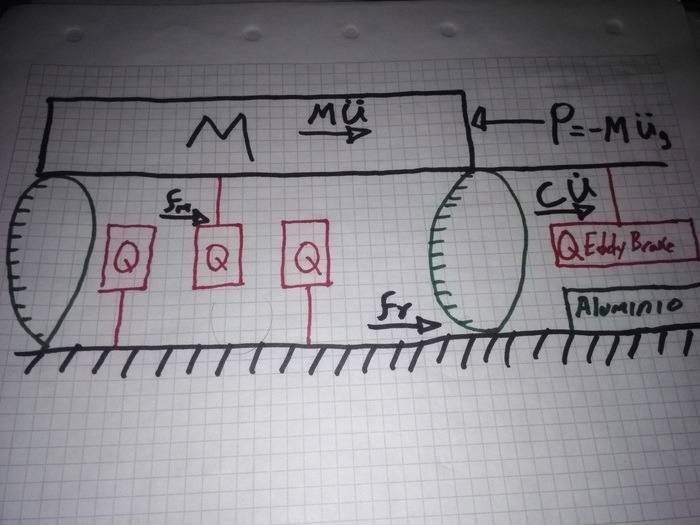
Sorry, my hands are kinda stupid; in the image i draw only one restoring magnet adhered to the system, but the essence is the same: 'n' restoring magnets surrounded by 'n+1' magnets adhered in the other side.
in civil engineering school they teach us:
"the exciting force is equal to minus ground acceleration mass times"
As i describe in the image: 'P' (the exciting force) = -U"g*m (ground acceleration*system mass)
highlight: in structural engineering it is supossed to use a 'k' value which is the stiffness of the system. in those cases we say the building wants to 'restart' to it's 'zero' position with a force equal to: Fs=k*U.
in my case, as there is no columns or strings to the system, only magnets, i will say there is a magnetic force 'Fm' who wants to restart my system. this force is dependant of U and has values as showed in image 1.
the damping force: eddy brakes, in the literature I've read they say: Fd=C *U', where C equals to magnetic and geometric constants. have that equation ini mind please.
the inertial mass is simply: Fi=m*U", this is from second law of motion, you don't want to get sleepy reading about it.
friction force oposes every movement, i take it as: "if P-Fm-Fd-Fi<fr there will be no relative movement, because friction will not allow it"
so, summarizing forces i get:
m*U" + c*U' + Fm(U) + fr= -m*U"g
which is equal to:
U"=(-m*U"g - c*U' - Fm(U) - fr) / m
finnally that is what i am trying to solve in matlab's simulink
There is an extra force that is not specified in the diagram, this is the spheres's inertial force, there is 4 spheres of 1.5" and mass=0.2kg which supports the system. I calculated how much is this really important, and got: the mass of the system will increase in about 0.2kg. (so, not that much of importance)
now, the shaking table tests were really good, as expected, the system didn't shake as hard as the table did and everything was smooth, but now i have to build the system's MATLAB model... and man... this is dragging me nutz :v
I will share with you this test: table shakes with amplitude=10mm, frequency is increasing exponentially from 0.1hz to 5 hz.
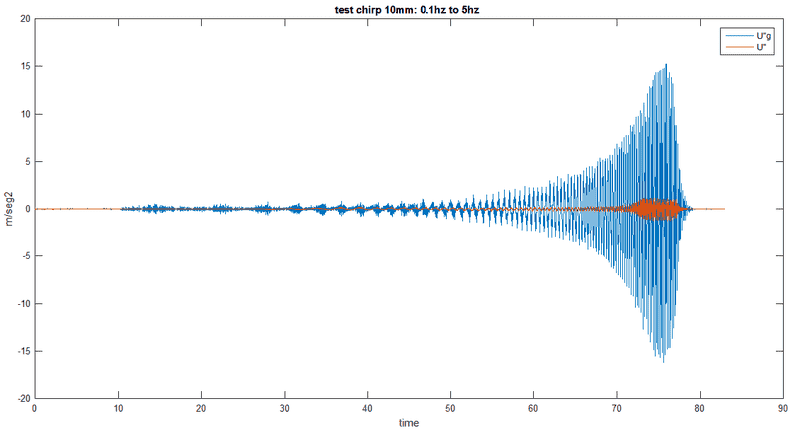
the image shows what accelerometers captured, before seg70 the system doesn't shake almost a thing. but, it starts shaking in (relatively) high frequencies with ~4.5hz. confused, i send that response to frequency domain and found:
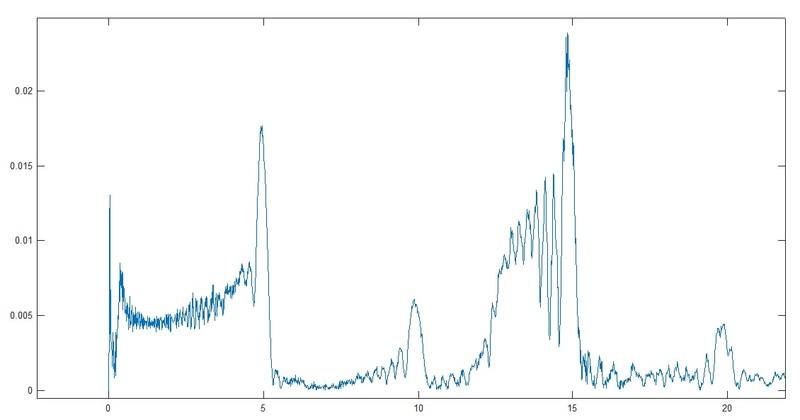
frequencies over the frequencies at which the table was shaking!
My attempts for solutions are made using matlab'simulink solving motion equation and optimizing damping 'c' value, got this:
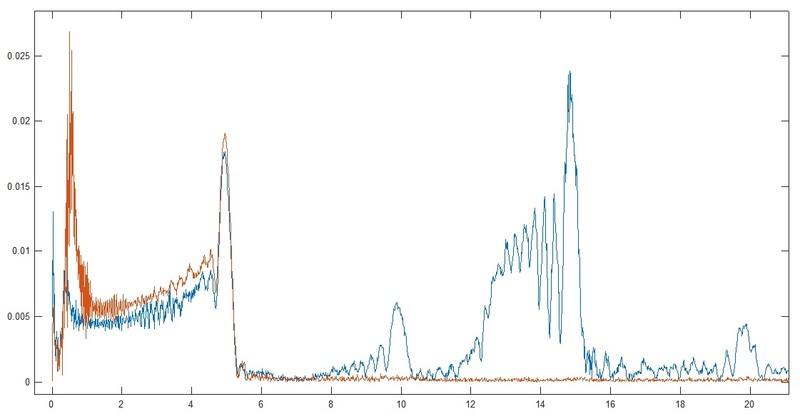
(My model is orange one) My model doesn't simulates frequencies over the ones at which the seismic table is shaking. this, in the time domain looks like this:
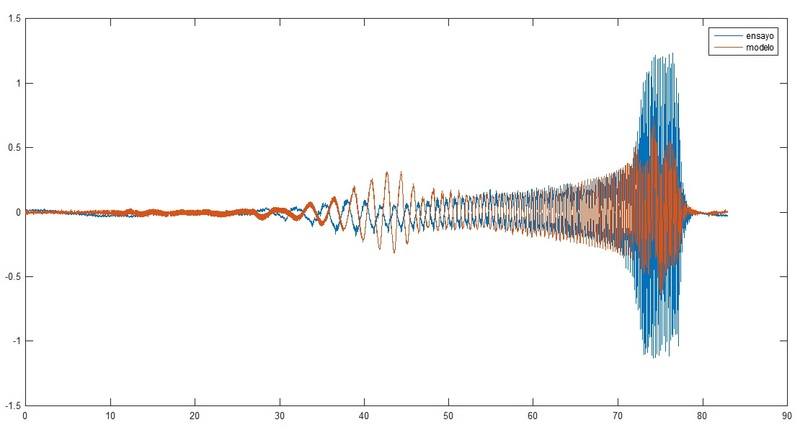
and if i make zoom at it:

(don't get confuse by time axis, it's the same graphic, i move the time but the idea is the same)
summarizing, i made the tests, i have to make the matlab's model, i can't figure out where those out of test frequencies are coming.
is there any other force i am not considerating?
Remember the 'c' value? i am taking it as constant, but now i am not pretty sure about it, maybe (just maybe) the problem comes with the called skin effect, but i don't know how to simulate it's equation.
pd:whoever reads this. thanks a lot even if you just read it out of curiosity
pd: sorry for bad english
Homework Statement
Before entering in details you (whoever you are) most know:
The system is scaled for obvious reasons. The system consists of a wood board (thickness=2", mass=17.34kg) which is over a seismic test table in laboratory. Between table and wood are the important things:
*steel spheres: support the weigh of the system vertically, rails under and over (seismic table shakes in one direction).
*restoring magnets: there is 3 magnets adhered to the seismic table and 4 adhered to the system. they are placed in patter to repulsive one with the other. this is made to restore the system to it's "zero"
*damping magnet: 3 (but united as 1) magnets are adhered in the system, an aluminium plate is placed below it and adhered to the seismic table. this will create eddy brakes and will "stop" the system from keep moving in the time.
(you will know what i am talking about in equations section)
The steel spheres most spin as the seismic table shakes, but, they have a rolling resistance. the transmissibility will be higher if the rolling resistance is it too. horizontal test throw a rolling resistance of fr=0.3N
As the magnetic force increases as the magnets are close between them, i did an force vs displacement static test, this is the result:
(result of horizontal test, load(N) vs relative displacement(mm))
dots means this is one direction test u+, as magnets are placed symmetrically u- is supossed to be equally.
Homework Equations
So, in here starts da big deal: here is the system diagram:
Sorry, my hands are kinda stupid; in the image i draw only one restoring magnet adhered to the system, but the essence is the same: 'n' restoring magnets surrounded by 'n+1' magnets adhered in the other side.
in civil engineering school they teach us:
"the exciting force is equal to minus ground acceleration mass times"
As i describe in the image: 'P' (the exciting force) = -U"g*m (ground acceleration*system mass)
highlight: in structural engineering it is supossed to use a 'k' value which is the stiffness of the system. in those cases we say the building wants to 'restart' to it's 'zero' position with a force equal to: Fs=k*U.
in my case, as there is no columns or strings to the system, only magnets, i will say there is a magnetic force 'Fm' who wants to restart my system. this force is dependant of U and has values as showed in image 1.
the damping force: eddy brakes, in the literature I've read they say: Fd=C *U', where C equals to magnetic and geometric constants. have that equation ini mind please.
the inertial mass is simply: Fi=m*U", this is from second law of motion, you don't want to get sleepy reading about it.
friction force oposes every movement, i take it as: "if P-Fm-Fd-Fi<fr there will be no relative movement, because friction will not allow it"
so, summarizing forces i get:
m*U" + c*U' + Fm(U) + fr= -m*U"g
which is equal to:
U"=(-m*U"g - c*U' - Fm(U) - fr) / m
finnally that is what i am trying to solve in matlab's simulink
There is an extra force that is not specified in the diagram, this is the spheres's inertial force, there is 4 spheres of 1.5" and mass=0.2kg which supports the system. I calculated how much is this really important, and got: the mass of the system will increase in about 0.2kg. (so, not that much of importance)
now, the shaking table tests were really good, as expected, the system didn't shake as hard as the table did and everything was smooth, but now i have to build the system's MATLAB model... and man... this is dragging me nutz :v
I will share with you this test: table shakes with amplitude=10mm, frequency is increasing exponentially from 0.1hz to 5 hz.
the image shows what accelerometers captured, before seg70 the system doesn't shake almost a thing. but, it starts shaking in (relatively) high frequencies with ~4.5hz. confused, i send that response to frequency domain and found:
frequencies over the frequencies at which the table was shaking!
The Attempt at a Solution
My attempts for solutions are made using matlab'simulink solving motion equation and optimizing damping 'c' value, got this:
(My model is orange one) My model doesn't simulates frequencies over the ones at which the seismic table is shaking. this, in the time domain looks like this:
and if i make zoom at it:
(don't get confuse by time axis, it's the same graphic, i move the time but the idea is the same)
summarizing, i made the tests, i have to make the matlab's model, i can't figure out where those out of test frequencies are coming.
is there any other force i am not considerating?
Remember the 'c' value? i am taking it as constant, but now i am not pretty sure about it, maybe (just maybe) the problem comes with the called skin effect, but i don't know how to simulate it's equation.
pd:whoever reads this. thanks a lot even if you just read it out of curiosity
pd: sorry for bad english