Discussion Overview
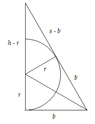
The discussion revolves around finding the smallest possible area of an isosceles triangle that can contain a circle of radius $r$ inscribed within it. Participants explore various mathematical approaches, including coordinate geometry and the relationship between the triangle's dimensions and the inscribed circle.
Discussion Character
- Exploratory
- Mathematical reasoning
- Technical explanation
- Debate/contested
Main Points Raised
- One participant seeks hints on the relationship between the inscribed circle and the triangle, considering similar triangles as a potential approach.
- Another participant describes using coordinate geometry to define the triangle and its area as a function of its dimensions, proposing a method to find constraints based on the intersection of a line and the circle.
- Participants discuss the equation of the line forming one side of the triangle and confirm its correctness through exchanges.
- There is a focus on deriving the equation of the circle and the upper half of the circle as a function, with some participants expressing uncertainty about the steps involved.
- Several participants engage in algebraic manipulations to derive relationships between the triangle's height and base, discussing the implications of the discriminant being zero for the quadratic formed.
- One participant expresses difficulty in isolating variables and discusses the implications of dividing by variables in the context of potential missing solutions.
- There is a mention of optimizing the area function and exploring critical values, with one participant suggesting a simplification by optimizing the square of the area function.
- Another participant references an external solution to the problem, indicating a different method was used, and requests clarification on that approach.
- Follow-up questions are raised regarding the significance of critical values and the type of triangle involved in the external solution.
Areas of Agreement / Disagreement
Participants generally engage in a collaborative exploration of the problem, with some expressing uncertainty and seeking confirmation on various steps. There is no clear consensus on the best approach or final answer, as multiple methods and interpretations are discussed.
Contextual Notes
Participants note the importance of the discriminant in determining the relationship between the triangle's dimensions and the inscribed circle, as well as the potential for missing solutions when dividing by variables. The discussion includes unresolved algebraic steps and varying interpretations of the problem.
Who May Find This Useful
Readers interested in mathematical optimization, geometry, and the relationships between shapes and inscribed figures may find this discussion relevant.