squenshl
- 468
- 4
Homework Statement
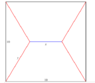
A wire pattern is inserted into a ##10##cm square by making a horizontal line in the middle of the square (not all the way across and with length ##x##) and connecting the ends of this line to the closest two corners. What is the minimum value of ##x##?
Homework Equations
The Attempt at a Solution
Let ##y## be the length of the wire from the end of ##x## to the corner of the square. This means the total length of the wire is ##l = x+4y##.
I extended the blue line ##x## to create a triangle then I used Pythagoras' to get ##y^2 = 25+\frac{(10-x)^2}{4}##.
Do I then throw this (meaning ##y##) into ##l## then differentiate with respect to ##x## then solve to get my minimum value for ##x## then ##y## which would give me the minimum length for ##l##.
Thanks!