Minimum work to transport electron?

[qlzlahs]

Homework Statement

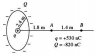
A charge Q = -820 nC is uniformly distributed on a ring of 2.4 m radius. A point charge q = +530 nC is fixed at the center of the ring. Points A and B are located on the axis of the ring, as shown in the figure. What is the minimum work that an external force must do to transport an electron from B to A?
(e = 1.60 × 10^-19 C, k = 1/4πε_0 = 8.99 × 10^9 N · m^2/C^2)

https://www.physicsforums.com/attachments/work-png.93021/?temp_hash=3fc763fb95a2d9ab71f3bf4a54a23c14

Homework Equations

V = (k*q)/(sqrt(R^2 + z^2))
work = (V_b - V_a)*q
work = (k*q_1*q_2)/r

The Attempt at a Solution

V_B = (9*10^9*530*10^(-9))/(3.2) = 1490.625 V
V_A = (9*10^9*530*10^(-9))/(1.8) = 2650 V
V_B - V_A = -1159.375 V

(V_B - V_A)*q, where q = 1.60*10^-19 C
(-1159.375)*(1.60*10^-19) = -1.855*10^-16 J

I'm not sure if I'm supposed to use -820 nC or 530 nC for the q value when calculating V_B or V_A.

 

[TSny]

V_B = (9*10^9*530*10^(-9))/(3.2) = 1490.625 V

Does the ring also contribute to the potential at point B?

 

[qlzlahs]

Does the ring also contribute to the potential at point B?

I was assuming that if the ring contributes to the potential at point A, it would to point B as well.

 

[TSny]

I was assuming that if the ring contributes to the potential at point A, it would to point B as well.

The same amount at both points?

 

[qlzlahs]

So.. How do I know how much potential there is at point B?

 

[TSny]

Look at your list of relevant equations.

 

[qlzlahs]

Look at your list of relevant equations.

Do I use the equation V = (k*q)/(sqrt(R^2 + z^2)) for both points A and B? With R = 2.4 and z = 1.8 for A, and z = 3.2 m for B?

 

[azizlwl]

Coulomb's law, F=kQ1Q2/r^2
Work=Fr
Since F is not constant between A and B, we have to calculate based on small distances dr so that F is constant within it.
dW=F(r)dr

Edit
You have to apply Gauss law too for the ring.

 

[Potatochip911]

Coulomb's law, F=kQ1Q2/r^2
Work=Fr
Since F is not constant between A and B, we have to calculate based on small distances dr so that F is constant within it.
dW=F(r)dr

Edit
You have to use Gauss law too for the ring.

Why would he want to use Gauss's law for this question? Work is equal to change in potential energy since $\Delta K=0$, i.e. $W=\Delta U=q\Delta V$, in this case $q$ is the electron. Note that for continuous charge distributions(Like the ring of charge): $V=\frac{1}{4\pi\varepsilon_0}\int\frac{dq}{r}$