Missing component to get the impendance ohmic

[Lindsayyyy]

Homework Statement

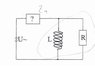
Hi, following graphic is given (attachment)

Homework Equations

-

The Attempt at a Solution

I tried it with the following equation:

$$\omega iL-\frac i {\omega C} + X =R$$

but I don't get to the solution, is this the right attempt? If yes, I'll try later on again, have to go to the university right now.

Thanks for the help

 

[cupid.callin]

what is the question?

 

[Lindsayyyy]

ah sorry, I was in a hurry. I shall find the missing component so that the impendance/resistance of the series connection is just ohmic

 

[ehild]

L and R are parallel. What is their resultant impedance?

ehild

 

[cupid.callin]

L and R are parallel. What is their resultant impedance?

ehild

Will that work?
the unknown resistance is also the part of LR circuit

 

[Lindsayyyy]

The impendance is:

$$\frac 1 Z = \frac 1 {i\omega L} - \frac {\omega C} {i}$$

Do I have to solve it afterwards with the equation

$$R=X+Z$$

And find the X ?

 

[cupid.callin]

what is C?

 

[ehild]

The impendance is:

$$\frac 1 Z = \frac 1 {i\omega L} - \frac {\omega C} {i}$$

Do I have to solve it afterwards with the equation

$$R=X+Z$$

And find the X ?

That box in the figure is not a capacitor but a resistor R connected parallel to the inductor. And yes, Z+X has to be real.

ehild

 

[Lindsayyyy]

Sorry everyone, I'm totally asleep at the switch, having exams in a few days and things are getting confused. I'll try it lateron, have so solve some other things first.

@ Cupid, I don't have any idea why I thought there's a capacity. maybe I should better look at the drawing

thanks everyone

 

[Lindsayyyy]

I'm stuck, can't solve it.

I tried to calculate Z, my Z is the parallel connection between R and L

and I get for Z:

$$\frac 1 Z = \frac 1 R + \frac {1} {i \omega L}$$

after some conversions I get to:

$$Z= \frac {R\omega^{2}L+iR^{2}\omega L} {R^{2}+\omega L^{2}}$$

Now I want to get a pure ohmic resistance so

$$Z+X=R$$

but I just can't solve it. The task says the missing component is a "normal" one, so I guess it should be a capacity, inductor etc. Though I tried to take one of these to test if I get a solution, I don't get to an answer. Can anyone help me

 

[gneill]

I'm stuck, can't solve it.

I tried to calculate Z, my Z is the parallel connection between R and L

and I get for Z:

$$\frac 1 Z = \frac 1 R + \frac {1} {i \omega L}$$

after some conversions I get to:

$$Z= \frac {R\omega^{2}L+iR^{2}\omega L} {R^{2}+\omega L^{2}}$$

Check your algebra. The ω in the term in the denominator should be squared, and the L in the real portion of the numerator should also be squared.

Once you've sorted that out, divide the expression into two parts: the real part and the imaginary part. It's the imaginary part that you want to "take care of" with the new impedance X.

 

[Lindsayyyy]

Hope I haven't done any mistakes again:

$$X=R- \frac {R\omega^{2}L^{2}} {R^{2}+\omega^{2}L^{2}} - \frac {iR^{2}\omega L} {R^{2}+\omega^{2}L^{2}}$$

so in order to get a pure ohmic term my X has to be:

$$X= \frac {iR^{2}\omega L} {R^{2}+\omega^{2}L^{2}}$$

but what component is that? I don't get it :(

 

[gneill]

Hope I haven't done any mistakes again:

$$X=R- \frac {R\omega^{2}L^{2}} {R^{2}+\omega^{2}L^{2}} - \frac {iR^{2}\omega L} {R^{2}+\omega^{2}L^{2}}$$

so in order to get a pure ohmic term my X has to be:

$$X= \frac {iR^{2}\omega L} {R^{2}+\omega^{2}L^{2}}$$

but what component is that? I don't get it :(

If you let Z be the impedance of the parallel R and L components, then you've found that

$$Z = \frac {R\omega^{2}L^{2}} {R^{2}+\omega^{2}L^{2}} + i\frac {R^{2}\omega L} {R^{2}+\omega^{2}L^{2}}$$

In order to cancel the imaginary term you need to put in series an impedance that is its negative, that is,

$$X = - i\frac {R^{2}\omega L} {R^{2}+\omega^{2}L^{2}}$$

Now, what sort of component has an impedance that yields a negative imaginary term?

 

[Lindsayyyy]

I'd say capcity with:

$$R_{C}=-\frac i {\omega C}$$

if that answer is right, I still don't understand why to use this one

 

[gneill]

I'd say capcity with:

$$R_{C}=-\frac i {\omega C}$$

if that answer is right, I still don't understand why to use this one

Yes, a capacitor gives a negative imaginary impedance.

If you set the above expression for a capacitor's impedance equal to the X expression then you can solve for C, the value that the capacitor must have in order to cancel out the imaginary term of the impedance in Z at a given frequency ω.

 

[Lindsayyyy]

Ok, thank your very much