stripes
- 262
- 0
I've successfully modeled a quadruple linked pendulum in Mathematica. I've done a few interesting things with the simulation. I've shown angles vs. time, and how a tiny change in initial conditions result in a completely different, unpredictable path for the masses of the pendulum. I've shown how the time for the farthest mass to "completely change path" itself changes with initial condition. I've shown how the "time for the farthest mass to flip" changes with initial condition. Now I'm plotting something like this:

Wikipedia explains this as follows: "Graph of the time for the [double] pendulum to flip over as a function of initial conditions" (see https://en.wikipedia.org/wiki/Double_pendulum#Chaotic_motion for more details). Now I've replicated this quite well (this is for the double pendulum):
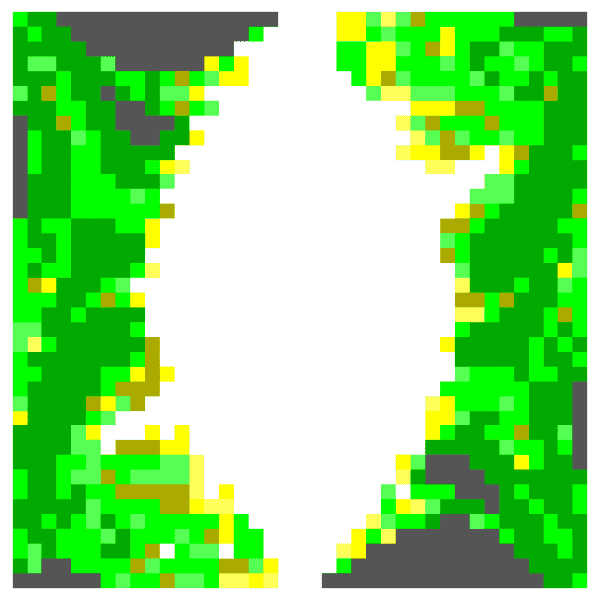
although it looks upside down in mine...not sure if I've reversed something...hmm.
Anyways, I'm looking for similar patterns in the quadruple pendulum. The biggest caveat is that there are now four initial angles to change, and plots above only have 2 dimensions. So I've been playing around with which of the two to vary, and which two to leave constant. I've also tried setting all four initial angles to vary with only two angles (like theta1 = theta3 and theta2=theta4). I haven't been able to get anything interesting to show up, except in the case where theta1=theta2 and theta3=theta4...which is basically like a double pendulum:
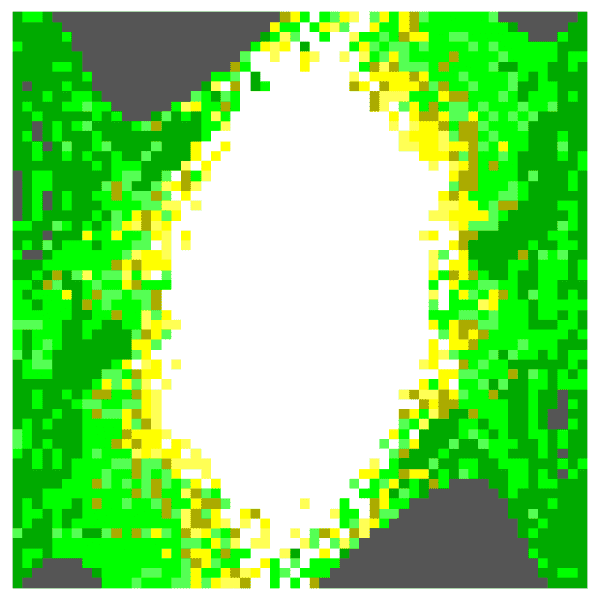
and it's not a whole heckuva lot different. (It also took about 30 minutes to draw that.) It's less symmetrical, which is expected.
So my question is: if I can only plot two angles (as above), but I have four initial angles to play with, is there any combination I should adjust that might lead to an interesting pattern? More generally, are there any other "Interesting" questions that I can talk about now that I have the simulated model (I have things like the momentum, angles all as a function of time). Thanks in advance!
Wikipedia explains this as follows: "Graph of the time for the [double] pendulum to flip over as a function of initial conditions" (see https://en.wikipedia.org/wiki/Double_pendulum#Chaotic_motion for more details). Now I've replicated this quite well (this is for the double pendulum):
although it looks upside down in mine...not sure if I've reversed something...hmm.
Anyways, I'm looking for similar patterns in the quadruple pendulum. The biggest caveat is that there are now four initial angles to change, and plots above only have 2 dimensions. So I've been playing around with which of the two to vary, and which two to leave constant. I've also tried setting all four initial angles to vary with only two angles (like theta1 = theta3 and theta2=theta4). I haven't been able to get anything interesting to show up, except in the case where theta1=theta2 and theta3=theta4...which is basically like a double pendulum:
and it's not a whole heckuva lot different. (It also took about 30 minutes to draw that.) It's less symmetrical, which is expected.
So my question is: if I can only plot two angles (as above), but I have four initial angles to play with, is there any combination I should adjust that might lead to an interesting pattern? More generally, are there any other "Interesting" questions that I can talk about now that I have the simulated model (I have things like the momentum, angles all as a function of time). Thanks in advance!

