Modulus of the electric field created by a sphere

[Guillem_dlc]

Homework Statement

A sphere of radius $6\, \textrm{cm}$ is uniformly charged to its surface with a density $\sigma=(10/\pi)\, \textrm{nC/m}^2$. Calculate the modulus of the electric field at points $P$ and $P'$, which are at $3\, \textrm{cm}$ and $10\, \textrm{cm}$ respectively, in the center of the sphere. Express the result in $\textrm{V/m}$.
a) $E(P)=0,\,\, E(P')=1.3\cdot 10^2$
b) $E(P)=90,\,\, E(P')=1.7\cdot 10^2$
c) $E(P)=360,\,\, E(P')=0$
d) $E(P)=0,\,\, E(P')=86$

Relevant Equations

Gauss Law

I think the right solution is c). I'll pass on my reasoning to you:

R=6\, \textrm{cm}=0'06\, \textrm{m}
\sigma =\dfrac{10}{\pi} \, \textrm{nC/m}^2=\dfrac{1\cdot 10^{-8}}{\pi}\, \textrm{C/m}^2
P=0'03\, \textrm{m}
P'=10\, \textrm{cm}=0,1\, \textrm{m}

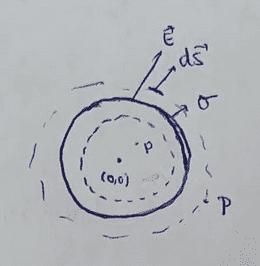
Point P:
<br /> \left.<br /> \phi =\oint E\cdot d\vec{S}=E\cdot S \atop<br /> \phi =\dfrac{Q_{enc}}{\varepsilon_0}=0<br /> \right\} E=0\Rightarrow E(P)=0
Point P':
\phi =\oint \vec{E}\cdot d\vec{S}=\oint E\cdot dS\cdot \underbrace{\cos \theta}_1=E\cdot \oint dS=E\cdot S
\phi =\dfrac{Q_{enc}}{\varepsilon_0}=\dfrac{\frac{1\cdot 10^{-8}}{\pi}\cdot S}{\varepsilon_0}\rightarrow \dfrac{\frac{1\cdot 10^{-8}}{\pi}}{\varepsilon_0}\cdot S=E\cdot S
E=\dfrac{\frac{1\cdot 10^{-8}}{\pi}}{8&#039;85\cdot 10^{-12}}=356&#039;67\approx \boxed{360\, \textrm{N/C}}

But in the solution it says that the correct answer is a).

 

[BvU]

You find 0 for $P$ and still think the right answer is c) ?

 

[BvU]

And for point $P'$ The distance from the center of the sphere is irrelevant ?

 

[Delta2]

First of all when we going to use Gauss's law in electrostatics in a problem like this, we have to also refer to any symmetries that are present in the problem. In this problem we have spherical symmetry of the electric field inside and outside the sphere.
Having that in mind:
Your reasoning and result for $E(P)=0$ seems correct to me.

Your reasoning for $E(P')$ would be correct if $P'$ was lying at the surface of the sphere of radius 6cm, and in this case the two $S$ that are present in the equation
$$\frac{\frac{1 \times 10^8}{\pi}}{\epsilon_0}\cdot S=E\cdot S$$

are indeed the same $S$.

BUT

because the point P' is at distance 10cm from the center of the sphere of radius 6cm, the two S that are appearing in this equation are not indeed the same S (why?)

 

[BvU]

Giving away the clue, eh ?

 

[Delta2]

Ok I ll edit my post fast!