Xyius
- 501
- 4
I am confused about one thing on this derivation. Okay so the guide I am following goes like this..
-------------------------------------
\sigma=\frac{M}{A}
dm=\sigma dA=(\frac{M}{4\pi R^2})2\pi rsin\phi Rd\phi
dm=\frac{M}{2}sin\phi d\phi
This is one part that confuses me. It seems as though the lower case "r" was used to cancel out one of the "R's" on the bottom. I can't reason another way how it went away. The rest of the derivation goes like this.. (Just in case anyone needs it)
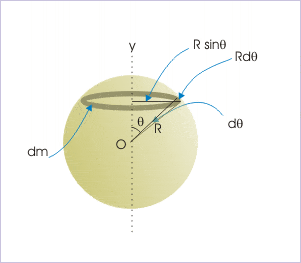
Here, radius of elemental ring about the axis is R sinθ. Moment of inertia of elemental mass is :
Therefore the total moment of inertia is..
The limits are 0 to \pi hence..
-------------------------------------
\sigma=\frac{M}{A}
dm=\sigma dA=(\frac{M}{4\pi R^2})2\pi rsin\phi Rd\phi
dm=\frac{M}{2}sin\phi d\phi
This is one part that confuses me. It seems as though the lower case "r" was used to cancel out one of the "R's" on the bottom. I can't reason another way how it went away. The rest of the derivation goes like this.. (Just in case anyone needs it)
Here, radius of elemental ring about the axis is R sinθ. Moment of inertia of elemental mass is :
dI=R^2sin^2\phi dm=R^2sin^2\phi (\frac{M}{2}sin\phi d\phi)
Therefore the total moment of inertia is..
\oint R^2sin^2\phi (\frac{M}{2}sin\phi d\phi)
\frac{MR^2}{2}\oint sin^3\phi d\phi = \frac{MR^2}{2}\oint (1-cos^2\phi )sin\phi d\phi = \frac{MR^2}{2}\oint sin\phi - sin\phi cos^2\phi d\phi = \frac{MR^2}{2}(-cos\phi +\frac{1}{3} cos^3\phi )
\frac{MR^2}{2}\oint sin^3\phi d\phi = \frac{MR^2}{2}\oint (1-cos^2\phi )sin\phi d\phi = \frac{MR^2}{2}\oint sin\phi - sin\phi cos^2\phi d\phi = \frac{MR^2}{2}(-cos\phi +\frac{1}{3} cos^3\phi )
The limits are 0 to \pi hence..
I=\frac{2}{3}MR^2