dp_033
- 3
- 0
Hey there!
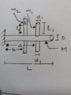
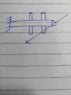
I am working on a project concerning the mathematical modeling of nano-swimmers in a viscous medium. Assuming the nano-swimmers to be cantilever beams, the project involves calculation of moment of inertia of the said nano-swimmers. While calculating the moment of inertia of a simple or a tapered cantilever beam is quite easy, I was facing problems dealing with a branched cantilever beam. The branches are placed in pairs and each pair has the same dimensions, protrude at the same distance from the support and face the opposite direction from each other. Any sort of help would be appreciated!
I am working on a project concerning the mathematical modeling of nano-swimmers in a viscous medium. Assuming the nano-swimmers to be cantilever beams, the project involves calculation of moment of inertia of the said nano-swimmers. While calculating the moment of inertia of a simple or a tapered cantilever beam is quite easy, I was facing problems dealing with a branched cantilever beam. The branches are placed in pairs and each pair has the same dimensions, protrude at the same distance from the support and face the opposite direction from each other. Any sort of help would be appreciated!