Moment and force calculation for cantilever beam

[Haye]

Homework Statement

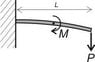
A cantilever beam (prismatic, rectangular cross section) is loaded at the tip by a force
P and at half its length L by a moment M.

a. Calculate the reaction force and moment.
b. Draw the shear force and bending moment diagrams

Homework Equations

∑F=0; ∑M=0

The Attempt at a Solution

a) The reaction force should be -P, so that the total force is zero. But I am not sure if it works the same for the moment, because I think the moment should always be calculated around the same point? Or should the reaction moment just be -M?
b) The shear force I calculated by looking at just a part of the beam, from somewhere in the middle completely to the right. Since it's total force should be zero, I think the shear force would be -P (positive shear is defined as if it would rotate the piece clockwise)
But for the bending moment diagram, I am at a complete loss. I know it should be zero at the right end, but I don't know what I would get at the left and how the moment at the middle is reflected in the diagram.

I hope I made my thoughts clear, any help would be greatly appreciated.

 

[SteamKing]

In all such problems, don't try to eyeball the solution: draw the free body diagram and solve for the unknown reactions using the equations of static equilibrium. This will save you a lot of mental turmoil. Plus, in order to draw the shear force and bending moment diagrams, you'll have to do this anyway.

 

[haruspex]

I am not sure if it works the same for the moment, because I think the moment should always be calculated around the same point? Or should the reaction moment just be -M?

Would there be a reaction moment at the wall if you took away M and just had P?

 

[Haye]

In all such problems, don't try to eyeball the solution: draw the free body diagram and solve for the unknown reactions using the equations of static equilibrium. This will save you a lot of mental turmoil. Plus, in order to draw the shear force and bending moment diagrams, you'll have to do this anyway.

Would there be a reaction moment at the wall if you took away M and just had P?

I did draw the free body diagram, but I have a lot of trouble understanding the concept of moment.
There should be a reaction moment at the wall even without P I just realized; this reaction moment has to cancel PL. But I find it really hard to see what I need to do with the moment M.
Would the reaction moment then be -PL-M?

Thank you both for the reply.

 

[SteamKing]

I did draw the free body diagram, but I have a lot of trouble understanding the concept of moment.
There should be a reaction moment at the wall even without P I just realized; this reaction moment has to cancel PL. But I find it really hard to see what I need to do with the moment M.
Would the reaction moment then be -PL-M?

Thank you both for the reply.

It's very simple. In the sum of the forces equation, you only include forces. In the sum of the moments equation, you only include moments due to applied forces and any applied moments.

Since the applied force P produces a moment in the same direction as M, then the moment reaction at the fixed end must be equal and opposite of the sum of these moments. It's also important to establish a positive direction for forces and moments in these problems.

 

[haruspex]

Would the reaction moment then be -PL-M?

Yes.

 

[Haye]

OK, thank you! I finally understand the problem. I really appreciate the help!