Momentum and impulse of a football

[ac7597]

Homework Statement

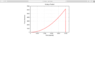
Joe Varsity kicks a football of mass 0.9 kg. As his foot makes contact with the ball, it exerts a force which gradually increases to a maximum value over 5 milliseconds, then falls immediately to zero, as shown in the graph above. The force is given by the equation:
Force=(250 Newtons)∗(t/t0)^2
where t0 equals 1 millisecond.

What is the impulse given by Joe's foot to the ball? Don't forget the units

The ball was originally sitting on the tee, motionless. What is its speed immediately after Joe kicks it?

Relevant Equations

average force= impulse/(time)

Homework Statement: Joe Varsity kicks a football of mass 0.9 kg. As his foot makes contact with the ball, it exerts a force which gradually increases to a maximum value over 5 milliseconds, then falls immediately to zero, as shown in the graph above. The force is given by the equation:
Force=(250 Newtons)∗(t/t0)^2
where t0 equals 1 millisecond.

What is the impulse given by Joe's foot to the ball? Don't forget the units

The ball was originally sitting on the tee, motionless. What is its speed immediately after Joe kicks it?
Homework Equations: average force= impulse/(time)

Since impulse= (average force)*time
average force= (250 Newtons)∗(0.005s /1 milliseconds)^2= 6250N
impulse= (0.005 s)(6250N)= 31.25 J
Is J the right unit or is it N*s ?

momentum= (mass)(velocity)
momentum immediately after Joe kicks the ball= (250 Newtons)∗(0.001s /1 milliseconds)^2 * (0.001s) = 0.250N
0.250N = (0.9kg)(velocity)
velocity=0.278 m/s

 

[Delta2]

I am afraid both of your answers are incorrect.

First what you calculate as average force, is NOT the average force at all, it is rather the maximum force which is the force at time t=0.005sec. Also I think that to find impulse you should integrate the force formula over the time interval of 0.005sec that is you should consider the integral $$\Omega=\int_0^{0.005}250\cdot (\frac{t}{t_0})^2dt$$
After you calculate that integral, use the momentum-impulse theorem that is
$$\Delta J=J_{after}-J_{before}=\Omega$$ and you should be able to calculate the momentum and the velocity of the ball after the kick.

 

[ac7597]

Ω= 250N(1/0.001)^2 ∫(t^2) dt
Ω=(250*10^6) * (t^3)/3 with t=0.005 and t=0
Ω=10.417-0=10.417N*s

10.417N*s= (0.9kg)(velocity)
velocity=11.57m/s
Thanks!