Morse Potenials Energy eigenvalues

[QuarkDecay]

TL;DR

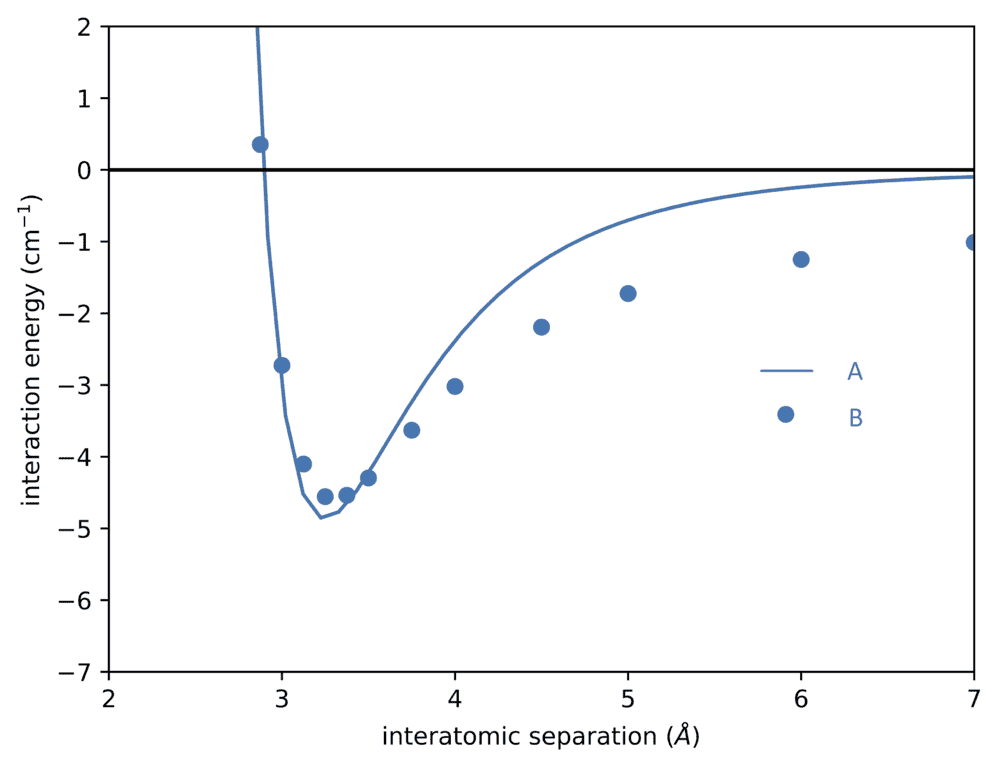
Two Morse potential like below are given. What are their energy eigenvalues?

I know the eigen value of energy in a Morse potential is
E_vib= ħω_o(v+ 1/2) - ħω_ox_e(v+ 1/2)²

but is this the same for every Morse potential, given that the masses μ of the diatomic molecules are the same?

The two potentials are these:

 

[hilbert2]

The parameters $\omega_0$ and $x_e$ depend on the parameters of the particular Morse potential, so it's not the same every time. That expression of the eigenvalues is also only an approximation that works for low energy states. If the energy is high enough, it's not even a discrete spectrum anymore.