SUMMARY
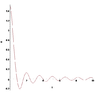
The discussion focuses on modeling the motion of a non-linear pendulum with air resistance using the equations Fc = mgsin(theta) and Fdrag = (1/2)p(v^2)CA. The user initially struggles with obtaining a damped oscillating curve due to the term v^2 not changing signs. After suggestions to replace v^2 with |v|v and correcting sign errors in the force equations, the user successfully adjusts their model, leading to improved graph outputs. The final equation derived is θ'' = -g/L sin(θ) - (pLcA/2m) θ' |θ'|, with initial conditions θ(0) = 1.5 and θ'(0) = 0.
PREREQUISITES
- Understanding of non-linear dynamics and pendulum motion
- Familiarity with air resistance modeling in physics
- Knowledge of differential equations and initial value problems (IVP)
- Proficiency in using mathematical software like Maple for solving equations
NEXT STEPS
- Explore the derivation of non-linear pendulum equations in detail
- Learn about numerical methods for solving initial value problems (IVP)
- Investigate the effects of varying parameters in air resistance models
- Study the application of absolute values in physics equations for damping effects
USEFUL FOR
Students and researchers in physics, particularly those studying dynamics, differential equations, and air resistance effects in mechanical systems.