DrunkenOldFool
- 20
- 0
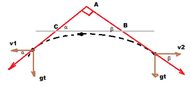
Two particles move in a uniform gravitational field with an acceleration $g$. At the initial moment the particles were located at one point and moved with velocities $v_1 = 3 \text{ms}^{-1}$ and $v_1 = 4 \text{ms}^{-1}$ horizontally in opposite directions. Find distance between the particles when their velocities become mutually perpendicular.