Multi-loop RC circuit, 2 batteries, 7 resistors, 1 capacitor

[physninj]

Homework Statement

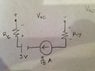
For the multi-loop circuit as shown, assuming the capacitor is initially uncharged, find the currents in each of the resistors at t=0 after the switches are closed.

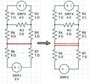
So I believe there are 8 unknowns really because of the 8th branch with the capacitor. If you look at the attached diagram 1, You can see what I mean. The problem asks for the currents across each resistor so I will use I_1-7 for the currents and R_1-7 for the resistances. I_cap is the current across the extra branch.

Homework Equations

ƩV=0 loop rule
ƩI=0 junction rule

V=IR

The Attempt at a Solution

Its a long process but I chose the directions I assumed the currents were moving in diagram 2.
The circuit has 4 junctions for which I have the following 4 equations.

I₁=I₃+I₄
I₃=I₂+I₅
I_cap=I₄+I₆
I₇=I_cap+I₅

Next, I used the loop rule. There are 6 possible loops, I wrote 4 equations, one for each of the three inner loops and one loop for the outside. Since capacitor is uncharged there is no resistance and current goes freely through it (correct?).

For the top loop, I took the current to be traveling counterclockwise and got:

ε₄-I₁R₁-I₃R₃-I₂R₂=0

Middle loop (taken clockwise)

-I₄R₄+I₅R₅+I₃R₃=0

Lower loop (clockwise)

ε₃-I₆R₆-I₇R₇=0

Finally I went clockwise around the outside of the circuit

ε₃-I₆R₆+I₄R₄+I₁R₁-ε₄+I₂R₂-I₅R₅-I₇R₇=0

I haven't even found a single example approaching this kind of complexity. I'm trying to keep from curling up in the fetal position and crying.

I am not sure about the directions of my currents, so I'm worried that there are problems in my equations above. Is this possible? I've been told it just comes out negative in the end. Its asking a lot I know, but can anybody tell if all these equations are right?

I haven't taken linear algebra, but I've been trying to make it into a matrix and I have no idea what I am doing there either. It seems pretty insurmountable with algebraic methods, but that's not really what I'm focused on right meow. I think I just want to know that what I'm doing so far is right, then I can worry about getting solutions to I_1-7. You are absolute lifesavers. Thank you.

 

[rude man]

1. Since capacitor is uncharged there is no resistance and current goes freely through it (correct?).

Right. Making the voltage across it how much?

The rest is not that bad. The current thru R6 & R7 is easy. Then, you can combine 3 resistors, put eh result in series with two other resistors, and you're done. You don't need to solve any KCL equations, just combine resistances in parallel & series etc.

 

[tiny-tim]

hi physninj!

So I believe there are 8 unknowns …

no, I₁ = I₂, and I₆ = I₇

… I chose the directions I assumed the currents were moving in diagram 2.

it doesn't matter what directions you choose

if you choose "wrong", the result for that current just comes out negative!

the only advantage of guessing "right" is that it makes a mistake very slightly less likely

… There are 6 possible loops, I wrote 4 equations, one for each of the three inner loops and one loop for the outside.

no, there's only 3 independent loops, so you can only write 3 independent equations …

(your outside loop equation is the sum of the other three)

just choose whichever three loops look easiest

 

[physninj]

Thank you both for your swift replies.

The voltage across the cap is 0.

It looks like I've been making things harder then they need to be, which is my specialty. That is a huge relief. Can't believe I wrote out an 8*9 matrix for this :P

Now I see that I2 has to equal I1 and likewise for I6 and I7. Is that because current in has to equal the current out of the batteries? why would that be? I think I can see how otherwise it would mess with the potentials and the charge wouldn't be conserved.

The question still remains about finding equivalent resistances, I didn't think that was possible with two EMF sources.

OOH independent loops eh? doesn't that just leave the three inner loops to work with? I feel much better about this problem already.

 

[ehild]

You can find the Thevenin equivalent voltage source between the capacitor plates, and then you have a simple RC circuit.

ehild

 

[physninj]

You've all been helpful, but I'm not sure where to go now. Ehild I studied up on Thevenin's theorem because it hasn't been covered in my class. Here is my latest work.

Starting with the lower loop I think I got I₆₇!

ε₃-I₆₇R₆-I₆₇R₆=0

ε₃/(R₆+R₇)=I₆₇

=3/13 A

I don't know what to do next, I drew what I think would be where I would try to apply the thevenin equivalent starting with the V_oc for the open circuit. See attached for that. Now how to find the open circuit equivalent voltage, do I sum everything somehow?

Also, if there is a way to complete the problem without the Thevenin by continuing with KCL, I think it would be preferable. I'm not supposed to know how to use it, it's not in my book and not covered which I actually find peculiar. He might be impressed, but I don't want to risk his reaction on the exam.

 

[rude man]

Stop it with the fancy equations already! Look at the diagram. What by inspection is the current thru R6 and R7 at t=0?

 

[physninj]

Stop it with the fancy equations already! Look at the diagram. What by inspection is the current thru R6 and R7 at t=0?

I think my way worked fine, the voltage divided by the total resistance in the bottom loop works out the same way, Is that what you are getting at? I kind of forgot about that equation. I simulated it and 3/13 is right, I just thought about it and now i see its just the voltage over the resistance.

I still don't understand the method you would take, can you at least tell me how having two EMF's doesn't require KCL?

 

[rude man]

I think my way worked fine, the voltage divided by the total resistance in the bottom loop works out the same way, Is that what you are getting at? I kind of forgot about that equation. I simulated it and 3/13 is right, I just thought about it and now i see its just the voltage over the resistance.

I still don't understand the method you would take, can you at least tell me how having two EMF's doesn't require KCL?

You have a voltage source EMF3 in series with two resistors R6 and R7 so what's the current? What does it matter if there is a second voltage source? It has nothing to do with the current in R6 and R7!

Then use the same method for the other side of the circuit. There you'll have to do some parallel'ing and series'ing like (R4 + R5)||R3 etc. but the idea is the same.

The "shorted" C acts as as a wall between R1-R5 and R6, R7.

BTW there's nothing wrong with writing the KCL's. It's just a whole lot of extra work.

 

[physninj]

You have a voltage source EMF3 in series with two resistors R6 and R7 so what's the current? What does it matter if there is a second voltage source? It has nothing to do with the current in R6 and R7!

Then use the same method for the other side of the circuit. There you'll have to do some parallel'ing and series'ing like (R4 + R5)||R3 etc. but the idea is the same.

The "shorted" C acts as as a wall between R1-R5 and R6, R7.

BTW there's nothing wrong with writing the KCL's. It's just a whole lot of extra work.

I got it with the KCL's. Yeah I don't agree with you. Whatever your method is, it's just giving me a headache. Just finding the effective resistance doesn't give you the voltage across the resistor, for R3 for example. You keep saying the fact that there are two batteries doesn't matter, It does matter, because it changes the potential and then I can't just divide it by the resistance to give current.

I12=16/21
I3=4/7
I45=4/21
I67=3/13

Thanks.

 

[ehild]

The solution is correct, good job! I haven't read the problem carefully, sorry. The Thevenin method was not a good idea. Rude man suggested to replace the capacitor with a short, a single wire as it has no resistance at the instant when the switches are closed. As the top circuit with the 4 V source shares a single wire with the lower circuit with the 3 V source, you can consider them as independent circuits.The currents can be obtained also by determining the equivalent resistances and applying Ohm's Law, but the KCL-s are also proper.

ehild

 

[physninj]

The solution is correct, good job! I haven't read the problem carefully, sorry. The Thevenin method was not a good idea. Rude man suggested to replace the capacitor with a short, a single wire as it has no resistance at the instant when the switches are closed. As the top circuit with the 4 V source shares a single wire with the lower circuit with the 3 V source, you can consider them as independent circuits.The currents can be obtained also by determining the equivalent resistances and applying Ohm's Law, but the KCL-s are also proper.

ehild

YES! Thank you so much! I see now that the current through the capacitor's branch is just I45+I67 and they otherwise behave like normal independant circuits. It could potentially be easier to solve that way. I'll give it a go, the first time was just practice. Thank you everyone.