timman_24
- 52
- 0
I am writing a multi-region diffusion code. The two regions have different material properties, so the analytical solution shows a discontinuity at the interface between the regions.
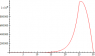
As can be seen here:

The numerical code I am running is (Mathematica):
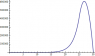
This works great if the material properties between the two regions are identical, but if I use differing material properties, I still get a smooth curve:

Is there a trick to getting this to work with finite difference method? How do I deal with this type of interface condition?
Thanks guys
As can be seen here:
The numerical code I am running is (Mathematica):
Code:
While[converge > .00001,
count = count + 1;
list1[[1]] = list1[[2]];
For[i = 2, i < Ai + 1, i++,
list1[[i]] = Dw (list1[[i - 1]] + list1[[i + 1]])/(H^2 Ea1 + 2 Dw)];
For[j = Ai + 1, j < (Ai + Bi), j++,
list1[[j]] = .5*(-H^2 (list1[[j]] Ea2/Dc - S/Dc) + list1[[j - 1]] +
list1[[j + 1]])];
converge = Max[Abs[list2 - list1]];
list2 = list1;]This works great if the material properties between the two regions are identical, but if I use differing material properties, I still get a smooth curve:
Is there a trick to getting this to work with finite difference method? How do I deal with this type of interface condition?
Thanks guys