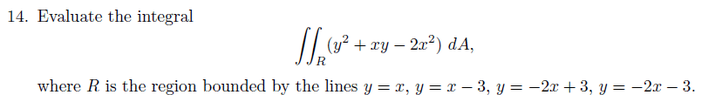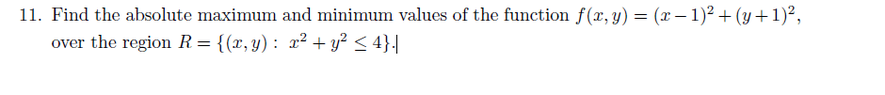Multiple Integral and Optimization in 3D

[Vanrichten]

View attachment 1691

In this problem I have drawn out the region specified and noticed two sets of parallel lines indicating to me that a change of variable(u and v) are able to be used to solve this integral.

I decided that u=y-x and v = -2x-y then solving for x and y I obtain x= (u-v)/3 and y = (4u-v)/3

From here I can compute the jacobian but I want to be sure the work above is correct before I move on. Can anyone please confirm?

For this second problem can anyone verify that it has been completed correctly

View attachment 1692

View attachment 1693

I think I have the right absolute minimum and maximum. Can someone also verify ?

 

[MarkFL]

I would work the second problem as follows:

We are given the function:

$$f(x,y)=(x-1)^2+(y+1)^2$$

Computing the first partials, and equating them to zero, we find:

$$f_x(x,y)=2(x-1)=0$$

$$f_y(x,y)=2(y+1)=0$$

This yields the critical point $(x,y)=(1,-1)$, which is within $R$. Using the second partials test for relative extrema, we find:

$$f_{xx}(x,y)=2$$

$$f_{yy}(x,y)=2$$

$$f_{xy}(x,y)=0$$

Hence:

$$D(x,y)=4$$

Since $$f_{xx}(1,-1)=2>0$$ and $$D(1,-1)=4>0$$ we conclude this critical value is a relative minimum.

$$f(1,-1)=(1-1)^2+(-1+1)^2=0$$

To check the boundary, we may use Lagrange multipliers.

The objective function is:

$$f(x,y)=(x-1)^2+(y+1)^2$$

subject to the constraint:

$$g(x,y)=x^2+y^2-4=0$$

and this yields the system:

$$2(x-1)=\lambda(2x)$$

$$2(y+1)=\lambda(2y)$$

which implies:

$$\lambda=\frac{x-1}{x}=\frac{y+1}{y}\implies y=-x$$

Substituting for $y$ into the constraint, there results:

$$x^2+(-x)^2=4$$

$$x=\pm\sqrt{2},y=\mp\sqrt{2}$$

Thus, the extrema values of the function on the boundary are:

$$f(\sqrt{2},-\sqrt{2})=(\sqrt{2}-1)^2+(-\sqrt{2}+1)^2=6-4\sqrt{2}$$

$$f(-\sqrt{2},\sqrt{2})=(-\sqrt{2}-1)^2+(\sqrt{2}+1)^2=6+4\sqrt{2}$$

Thus, the absolute extrema of $f$ over $R$ are:

$$f_{\min}=f(1,-1)=0$$

$$f_{\max}=f(-\sqrt{2},\sqrt{2})=6+4\sqrt{2}$$