- #1
Action_Man
- 6
- 0
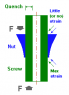
I'm trying to determine the contact surface area of a threaded bolt so that I can make some changes to the design and maintain the same contact surface so as not to affect the performace in other ways.
This presents itself as a helix, and my initial guess was that it may be best to work this out using a two or three stage integral incorporating the radius, rotation and translation along the axis, but I can't quite get my head around how it all fits together.
My main confusion lies in the starting point. I've pus my sketches below which will hopefully help. Any direction or further understanding anyone can offer on this would be great.
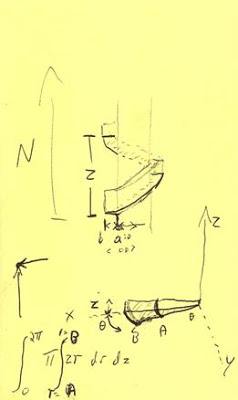
This presents itself as a helix, and my initial guess was that it may be best to work this out using a two or three stage integral incorporating the radius, rotation and translation along the axis, but I can't quite get my head around how it all fits together.
My main confusion lies in the starting point. I've pus my sketches below which will hopefully help. Any direction or further understanding anyone can offer on this would be great.