Homework Help Overview
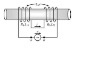
The discussion revolves around a circuit involving two inductors connected in series, characterized by their internal resistances and self-inductances, with a specified magnetic coupling factor. The original poster seeks to determine the mutual inductance between the inductors, given limited numerical information.
Discussion Character
- Exploratory, Assumption checking, Conceptual clarification
Approaches and Questions Raised
- Participants explore the implications of the magnetic coupling factor and question the significance of the sign of mutual inductance. There is discussion about the winding directions of the inductors and the concept of dot notation for coupled inductors. The original poster expresses confusion regarding the formulas for coupling inductors and seeks clarification on the dot notation.
Discussion Status
The discussion is ongoing, with participants providing insights into the dot notation and its relevance to understanding mutual inductance. Some participants suggest that additional information about the circuit is necessary to progress further, while others acknowledge the need for a symbolic result due to the lack of specific values.
Contextual Notes
Participants note that the problem lacks specific numerical values for the self-inductances and current, which constrains the ability to derive a complete solution. The original poster is also navigating the learning curve associated with the dot notation and its implications for mutual inductance.