Dot convention inductors in series: equation confusion

[Granger]

Homework Statement

So I'm really confused with mutual inductors and dot convention. If your answer is going to be a link to any website I can assure you I read them all and that only left me more confused. So here are my questions:

Homework Equations

3. The Attempt at a Solution [/B]
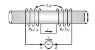
-> Should we write the absolute values of the mutual inductance? If so, why? Here is the example provided by my book:

They say that for the left side we have concordant coupling (mutual inductance positive) and therefore the series inductance is going to be:

$$L = L_{11} + L_{22} + 2 |L_M|$$

Why the use of the absolute value though? Isn't the coupling concordant and mutual inductance positive? What if it was negative, do you still have concordant coupling? I can see that if we apply the right-hand screw rule the fluxes have the same direction.

And for the right side discordant coupling (mutual inductance negative) and therefore the series inductance is going to be:

$$L = L_{11} + L_{22} - 2 |L_M|$$

Again: Why using the absolute value though? Isn't the coupling discordant (mutual inductance negative)? What if it was positive, do you still have discordant coupling? I can see that if we apply the right-hand screw rule the fluxes have opposite directions.

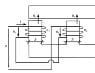
Next example my book provides is this one:

By applying the same thinking pattern of the previous one we have discordant coupling (mutual inductance negative) and therefore the series inductance is going to be:

$$L = L_{11} + L_{22} - 2 |L_M|$$

HOWEVER, my book now provides this:

$$L = L_{11} + L_{22} + 2 L_M$$

I know that because \$L_M\$ is indeed negative this will lead us to the same result, however, why remove the absolute value now? Or are they assuming concordant coupling even though the mutual inductance is negative? Or is there a step I'm missing? This one didn't bother me so much because I ended up with the same answer.

However, the final case is where I drop the ball:

So here I had previously calculated the mutual inductance and found out it was indeed negative. The series connection also suggests to me that we have discordant coupling (by dot convention) and therefore the series inductance is going to be:

$$L = L_{11} + L_{22} - 2 |L_M|$$

But now my book gives the answer:

$$L = L_{11} + L_{22} - 2 L_M$$

And since $L_M$ is negative this will originate different values.

I feel so confused right now, I have no idea how am I supposed to solve problems right this because I keep getting different answers. Can someone help me organize my line of thought. I think I understand concept of mutual inductance. What I don't understand is this thing with absolute values and series connection and I don't really know what to do.

 

[rude man]

Whew, didn't read it all But:
Mutual inductance can be + or - . If you have 2 coupled coils i and j, mutual inductance is M_ji = V_ji/dI_i/dt where V_ji is the voltage induced in coil j due to the current in coil i and I_i is the current in coil i. It is by no means easy to show that M_ij = M_ji but it's always true. So there is only one M (one L_M in your book. Your book uses L_M for mutual inductance; I prefer simply M).

Or you can look at it in terms of flux: V_ji = N_j dφ_ji/dt so that allows you to associate flux with mutual inductance.

In either case it should be apparent that the flux from one coil can generate a + or - voltage on the other coil depending on the mutual orientation of the coils. This means that mutual inductance can also be + or - by the above equations. . You surely know what the absolute sign | | does so there should be nothing more that needs saying.

Except to remind you that there is something called the dotting convention. Mutual inductance is + if + currents flow into both dotted ends of i and j. Etc.

 

[gneill]

Whenever I've seen a schematic with coupled inductances the mutual inductance is always given as a positive value. The dot notation allows you to sort out whether the mutual inductance is going to be "concordant" or "discordant" as you put it. As @rude man stated,

Mutual inductance is + if + currents flow into both dotted ends of i and j.

For your final case, look at the way the current flows through each inductor. It should be apparent that $\phi_2$ will be pointing in the opposite direction to what they've shown. Trace the path that the flux from coil one will take through the laminated core. Will it add to or subtract from the flux of coil 2?

 

[rude man]

Whenever I've seen a schematic with coupled inductances the mutual inductance is always given as a positive value.

But consider the expressions for a transformer:
V₁ = L₁ di₁/dt + M di₂/dt
V₂ = M di₁/dt + L₂ di₂/dt.
This I think is pretty standard form and M can of course be either + or - .

 

[gneill]

But consider the expressions for a transformer:
V₁ = L₁ di₁/dt + M di₂/dt
V₂ = M di₁/dt + L₂ di₂/dt.
This I think is pretty standard form and M can of course be either + or - .

I've seen them, but when I've seen schematics the M is always a positive value and the dot notation sorts out its sign. It may well be that your experience has been different.

 

[rude man]

I've seen them, but when I've seen schematics the M is always a positive value and the dot notation sorts out its sign. It may well be that your experience has been different.

OK. I haven't encountered any schematics with "M" or "L_M" designated thereon but I agree it does make more sense in those (rare?) cases.

 

[gneill]

OK. I haven't encountered any schematics with "M" or "L_M" designated thereon but I agree it does make more sense in those (rare?) cases.

Dunno about rare. It's what I've experienced. Much of that experience comes from my university exposure to circuit analysis, so it might well be a "localized" purview. I'd welcome other's input on their practical experience.