HumanistEngineer
- 18
- 2
- TL;DR
- Mutual thermal resistances between layers of a cylinder (either a pipe or a storage tank) in order to obtain heat transfer between these sections (e.g. from water to steel, steel to insulation, insulation to the ground and vice versa).
Ref: Palsson, Halldor | Analysis of Numerical Methods for Simulating Temperature Dynamics in District Heating Pipes - please check pg. 62 at LINK (CLICK!)
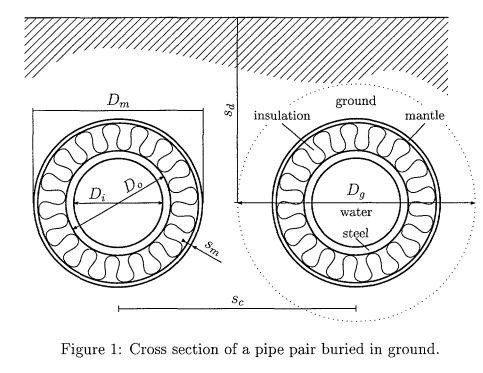
INTRO: In this reference, the mutual thermal resistances between layers as water-insulation, ground-surrounding, and insulation-ground are defined for a buried pre-insulated pipe, figure and formulations given below:
FIGURE:
FORMULATIONS:

QUESTION: I want to improve the model given in this reference by studying the layers as water, steel, insulation, and ground so I need to obtain the mutual thermal resistances between water-steel, steel-insulation, insulation-ground, and ground-surrounding. I couldn't find a reference describing how to find the thermal resistances between layers of a cylinder such as between water and steel and others. Can any of you help me either by giving formulations or by guiding me to a reference?
More details (Ri and Rg as given in the formulation above (3c)):
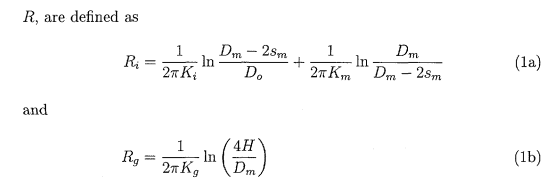
INTRO: In this reference, the mutual thermal resistances between layers as water-insulation, ground-surrounding, and insulation-ground are defined for a buried pre-insulated pipe, figure and formulations given below:
FIGURE:
FORMULATIONS:
QUESTION: I want to improve the model given in this reference by studying the layers as water, steel, insulation, and ground so I need to obtain the mutual thermal resistances between water-steel, steel-insulation, insulation-ground, and ground-surrounding. I couldn't find a reference describing how to find the thermal resistances between layers of a cylinder such as between water and steel and others. Can any of you help me either by giving formulations or by guiding me to a reference?
More details (Ri and Rg as given in the formulation above (3c)):