Discussion Overview
The discussion revolves around the derivation of wave speed on a string under tension, focusing on the angles involved in the forces acting on the string segments. Participants express confusion regarding the assumptions made about the angles between forces and the relationship between the angles and the geometry of the wave on the string.
Discussion Character
- Technical explanation
- Debate/contested
Main Points Raised
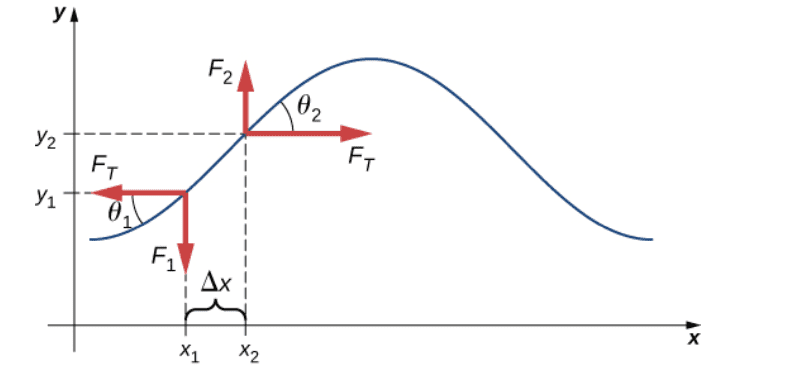
- Some participants question the assumption that the angles ##\theta_1## and ##\theta_2## represent the angles between the forces acting on the string, suggesting that these angles are derived from the geometry of the wave rather than the forces.
- There is a proposal to consider the x and y components of the force exerted on a segment of the string in terms of the tension and the angles, but this leads to further confusion about the definitions of these angles.
- One participant asserts that the force on each point of the string comes from adjacent segments, implying that the force direction is always parallel to the string itself.
- Another participant introduces a model using beads connected by rods to illustrate the concept of tension in the string, suggesting a limit approach to understand the continuous nature of the string.
Areas of Agreement / Disagreement
Participants do not reach consensus on the interpretation of the angles involved in the forces acting on the string. Multiple competing views remain regarding the relationship between the angles and the forces, as well as the assumptions made in the derivation.
Contextual Notes
There are unresolved questions about the definitions of the angles and the assumptions regarding the forces acting on the string segments. The discussion highlights the complexity of visualizing forces in a dynamic system like a vibrating string.