Need advice on diodes connected in series

[snoothie]

can someone advice me on how the graph should look like for a circuit with diodes connected in series?

Can we model the diodes this way?

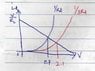
Attached picture shows the graphed charecteristic for 1 diode.

If its for 3 diodes, how should the graph look like?
Am i right to say that Vt will be 3 x 0.7v (Assuming the diode voltage drop is 0.7v) and value of Rd will be (3 x Rd) to model the resistance of the 3 diodes connected in series?

 

[es1]

Vt is right, and the gradient probably is as well.
As you put more elements in series you would expect the current to go down (gradient decrease, here you reduce it by 1/3 which makes sense).
However, I also suspect this model will loose accuracy pretty quickly as Vt increases.

 

[snoothie]

Hi es1,
Thanks for your advice.
Been searching for an answer to this for few days.

Will using the small signal ac resistance formula (Rd = nVT / Id) be more appropriate and accurate way of finding Rd?
If so is it applicable to a circuit that only has Dc voltage supply and no ac input?

Can someone advice me if my idea is correct?

 

[marcusl]

For an AC model the dynamic resistance triples for three series diodes as you deduced. At DC use the diode I-V relationship that you plotteed. Current through one or through three is identical, of course, but the voltage drop across all three (assuming they are identical) is 3 times the voltage for a single diode. To get the new graph from the graph for a single diode, then, just scale the V axis by three.

EDIT: BTW, you show a linear curve but that is not the correct I-V relation. It is
I=I_s*(exp(qV/kT)-1)
as you will see in any semiconductor device book.

EDIT: left out the "q" above...

 

[snoothie]

For an AC model the dynamic resistance triples for three series diodes as you deduced. At DC use the diode I-V relationship that you plotteed. Current through one or through three is identical, of course, but the voltage drop across all three (assuming they are identical) is 3 times the voltage for a single diode. To get the new graph from the graph for a single diode, then, just scale the V axis by three.

EDIT: BTW, you show a linear curve but that is not the correct I-V relation. It is
I=I_s*(exp(V/kT)-1)
as you will see in any semiconductor device book.

Thanks. looks like the graph posted in the 1st thread is now obsolete.

Am i right to say that the equation can also be used in a Dc only circuit? Still quite confused on this part, as i found this equation from an example with Ac supply added to Dc supply. So not quite sure if this equation is applicable with Dc only circuits.

I've posted another attachment of a sketch by hand of the new graph.
Please advice thanks.

I've done some working on it also. The given parameters:
n = 2
VT = 25.8mV
load resistance , RL = 1000 ohm
Vs = 10V

Worked Id = (10 - 2.1) / 1000 = 7.9mA
so i worked out the rd to be ... rd = (2 x 25.8mV) / 7.9mA = 6.53 ohm --> resistance for 1 diode in series?
And if above is correct, 3 x rd = 19.59 ohm ?
Can you advice me if this working is correct?
Thanks.

 

[marcusl]

Hmm, I'm not really a device guy, but I'll try to answer this. First, your revised curve looks right (although not drawn to scale...). The slope (tangent) to your curves where they cross the load line is the inverse dynamic resistance 1/Rd at your value of DC bias.

Here's how I would solve this, starting from first principles since that's what I know...:uhh: The diode equation I wrote is the equation for both AC and DC. If I add the emission factor (also called non-ideality factor) n as you have, and define V_T = kT/q as usual, then the I-V relation is
$$I=I_s(\exp{\frac{V}{nV_T }}-1) .$$
I think the reverse saturation voltage is around I_s=1e-9 A for a silicon diode, you should check it since it will affect the answer. At Vo=0.7V, n=2, the steady current is 0.7 mA.

Finding 1/Rd is equivalent to taking the derivative dI/dV evaluated at the bias point.
$$\frac{1}{R_d}=\frac{dI}{dV}=\frac{I_s}{nV_T } \exp{\frac{V}{nV_T }}$$
Invert both sides to get Rd. Evaluating at V=Vo=0.7V and plugging the other values in, I get 74 ohms.

EDIT: got the equations to render...

 

[marcusl]

Ok, I looked up a typical silicon diode, 1N914B, and the reverse leakage voltage is about 15 nA, not 1 nA as I assumed. Using this value for I_sat with your Vs and RL gives around 8.6 mA at 0.68V forward drop, close to the values you were given. Rd is then 5.2 ohms, or 15.6 ohms for 3 in series, also close to your values. It's nice when first principles give practical results! (Whew!)

I'd say your formula and results are correct for the values given in your problem.

 

[snoothie]

Hi Marcus,

Thanks for your great help.
Glad that I'm on track now.
Been slugging out this question for days...:yuck:

one thought, is it correct to say that when diodes are connected in series, we are pushing back the threshold voltage by 3 times (from 0.7v to 2.1v) in my case but when we find the Rd it is the equivalent dynamic resistance for 1 diode only?

 

[marcusl]

Well, the tangent slope changes so Rd for the series string is different than that for one diode.

If you want to know where the equation you quoted for Rd comes from, it's exactly the derivation I gave. My last equation above is your equation, in fact. Invert it as I mentioned above,
$$R_d=\frac{dV}{dI}=\frac{nV_T}{I_s \exp{\frac{V}{nV_T }}}.$$
The exponent term is 7e5 at V=0.7V, so there is no loss of accuracy to rewrite it as
$$R_d=\frac{dV}{dI}=\frac{nV_T}{I_s (\exp{\frac{V}{nV_T }}-1)}.$$
But the denominator is just the diode equation for I so
$$R_d=\frac{dV}{dI}=\frac{nV_T}{I}$$
which is exactly the equation you used. Sorry I didn't see this right away in my earlier post.