thatbluegsx90
- 1
- 0
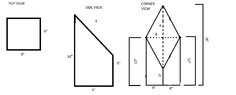
Not sure where exactly to post this but I think it fits in this category...I recently got interested in making a Terrarium and plan to make the glass enclosure myself.. for the life of me without having the physical thing in front of me I can't figure out one of the diagonal measurements of the top cover.. I apologize for the rough drawing but I'm looking for what A and B are(didn't mean to put the X in there)... I'm about 60% confident that B is 8 1/2 but I has been a while since I've done anything related to this