bancux
- 11
- 0
Dear all, I have difficulty in solving this problem (see the figure in attached thumbnails)
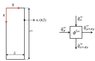
I have a rectangular shape with length/height of L and the thickness/width of \delta
Within the rectangular area, a heat conduction occurred. I would like to determine the temperature profile within the rectangular.
Based on the right hand side figure, I take a small cell with size of dx times dy. Applying the energy balance within the cell.
I have attached all the equation that I can think of, and also the boundary conditions. I have difficulty in solving the differential equation.
Thanks in advance.
note:
\lambda is thermal conductivity
\alpha is heat transfer coefficient, it is suppose to be dependent on x-location and time. I am going to simulate the heat transfer coefficient as a periodic function.
I have a rectangular shape with length/height of L and the thickness/width of \delta
Within the rectangular area, a heat conduction occurred. I would like to determine the temperature profile within the rectangular.
Based on the right hand side figure, I take a small cell with size of dx times dy. Applying the energy balance within the cell.
I have attached all the equation that I can think of, and also the boundary conditions. I have difficulty in solving the differential equation.
Thanks in advance.
note:
\lambda is thermal conductivity
\alpha is heat transfer coefficient, it is suppose to be dependent on x-location and time. I am going to simulate the heat transfer coefficient as a periodic function.