- #1
ObviousManiac
- 37
- 0
**PICTURE ATTACHED AT BOTTOM**
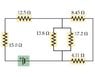
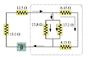
The current in the 13.8-Ω resistor in the attached picture is .795 A. Find the current in the other resistors in the circuit.
V=RI
In a series circuit:
V of Circuit = V1 + V2 + V3 +...Vn
I of Circuit = I1 = I2 = I3 = ...In
R of Circuit = R1 + R2 + R3 +... Rn
In a parallel circuit:
V of Circuit = V1 = V2 = V3 = ... Vn
I of Circuit = I1 + I2 + I3 +... In
1/R of Circuit = 1/(R1) + 1/(R2) + 1/(R3) +... 1/(Rn)
For the 13.8-Ω resistor, I found that Voltage = 10.971 by using V=IR
- Because V of Circuit = (V1 = V2 = V3 = ... Vn), the Voltage for the 17.2-Ω resistor is also 10.971
--Based on this, the Current for the 17.2-Ω resistor is .638:
V=IR
I=V/R
I=(10.971)/(17.2)
I=.638
After this, I proceeded to find the equivalent resistance for the entire circuit.
To find this, I separated the circuits into groups.
Group 1= the 15-Ω and 12.5-Ω resistors (they are in series).
Group 2= the 13.8-Ω and 17.2-Ω resistors (they are parallel).
Group 3= the 8.45-Ω and 4.11-Ω resistors (they are in series).
When solved for, the equivalent resistance for each group is as follows:
Group 1= 27.5-Ω
Group 2= 7.66-Ω
Group 3= 12.56-Ω
Note that Groups 2 and 3 are now parallel. We will combine them into Group 4.
Group 4 Resistance = 4.75-Ω
Now we only have Groups 1 and 4 left in series. When combined, we will get the net resistance for the entire Circuit. This works out to be 32.56-Ω
...So that's everything I could find, which is decent, but doesn't come anywhere near answering the question. I know I must be missing something somewhere.
How do I figure out the individual currents for each resistor with the information I currently have?
Homework Statement
The current in the 13.8-Ω resistor in the attached picture is .795 A. Find the current in the other resistors in the circuit.
Homework Equations
V=RI
In a series circuit:
V of Circuit = V1 + V2 + V3 +...Vn
I of Circuit = I1 = I2 = I3 = ...In
R of Circuit = R1 + R2 + R3 +... Rn
In a parallel circuit:
V of Circuit = V1 = V2 = V3 = ... Vn
I of Circuit = I1 + I2 + I3 +... In
1/R of Circuit = 1/(R1) + 1/(R2) + 1/(R3) +... 1/(Rn)
The Attempt at a Solution
For the 13.8-Ω resistor, I found that Voltage = 10.971 by using V=IR
- Because V of Circuit = (V1 = V2 = V3 = ... Vn), the Voltage for the 17.2-Ω resistor is also 10.971
--Based on this, the Current for the 17.2-Ω resistor is .638:
V=IR
I=V/R
I=(10.971)/(17.2)
I=.638
After this, I proceeded to find the equivalent resistance for the entire circuit.
To find this, I separated the circuits into groups.
Group 1= the 15-Ω and 12.5-Ω resistors (they are in series).
Group 2= the 13.8-Ω and 17.2-Ω resistors (they are parallel).
Group 3= the 8.45-Ω and 4.11-Ω resistors (they are in series).
When solved for, the equivalent resistance for each group is as follows:
Group 1= 27.5-Ω
Group 2= 7.66-Ω
Group 3= 12.56-Ω
Note that Groups 2 and 3 are now parallel. We will combine them into Group 4.
Group 4 Resistance = 4.75-Ω
Now we only have Groups 1 and 4 left in series. When combined, we will get the net resistance for the entire Circuit. This works out to be 32.56-Ω
...So that's everything I could find, which is decent, but doesn't come anywhere near answering the question. I know I must be missing something somewhere.
How do I figure out the individual currents for each resistor with the information I currently have?