Jeff.Nevington
- 12
- 1
- TL;DR
- Given three points on a positive definite quadratic line, I need to prove that the middle point is never higher than at least one of the other two.
Summary: Given three points on a positive definite quadratic line, I need to prove that the middle point is never higher than at least one of the other two.
I am struggling to write a proof down for something. It's obvious when looking at it graphically, but I don't know how to write the proof succinctly.
I have a positive definite quadratic equation:
y= (αx + φ)^2+x^2;
where x and y are the axes, and α and φ are real constants (could be positive or negative), so y is always ≥0.
If I choose three values of X: x_a, x_p, x_b, these will correspond to three values of y: y_a, y_p, y_b.
If x_a ≤ x_p ≤ x_b, it is obvious, visually on the curve that y_p ≤ y_a OR y_p ≤ y_b. Unfortunately I need something more robust than "obvious visually". Does anyone know how I would go about writing a mathematical proof for this?
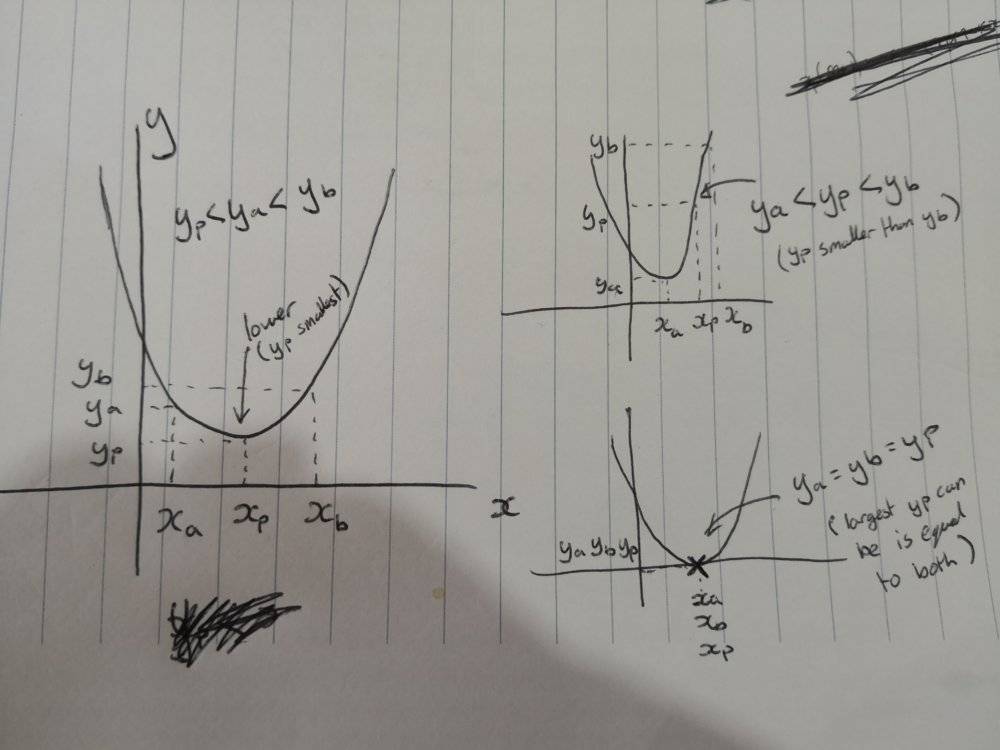
I am struggling to write a proof down for something. It's obvious when looking at it graphically, but I don't know how to write the proof succinctly.
I have a positive definite quadratic equation:
y= (αx + φ)^2+x^2;
where x and y are the axes, and α and φ are real constants (could be positive or negative), so y is always ≥0.
If I choose three values of X: x_a, x_p, x_b, these will correspond to three values of y: y_a, y_p, y_b.
If x_a ≤ x_p ≤ x_b, it is obvious, visually on the curve that y_p ≤ y_a OR y_p ≤ y_b. Unfortunately I need something more robust than "obvious visually". Does anyone know how I would go about writing a mathematical proof for this?