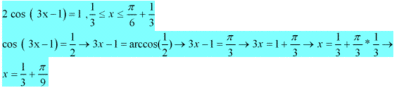Need Help With a Trigonometric Equation?

Click For Summary
SUMMARY

The discussion centers on solving the trigonometric equation involving the function cos(3x-1). It is established that the function repeats every 2π/3, indicating no additional solutions exist within the specified domain. Participants confirm that the solution for x is valid and fits within the restricted domain provided in the problem. Combining fractions is suggested but deemed unnecessary for the solution's completeness.

PREREQUISITES
  • Understanding of trigonometric functions, specifically cosine.
  • Knowledge of periodicity in trigonometric equations.
  • Familiarity with solving equations involving variables.
  • Basic algebraic manipulation skills.
NEXT STEPS
  • Study the periodic properties of trigonometric functions.
  • Learn how to solve trigonometric equations with multiple angles.
  • Explore the concept of restricted domains in trigonometric problems.
  • Practice combining fractions in algebraic expressions.
USEFUL FOR

Students studying trigonometry, educators teaching trigonometric equations, and anyone looking to enhance their problem-solving skills in trigonometric contexts.

siyanor
Messages
8
Reaction score
0
can somebody help me out on this one,i got stuck on this one
https://www.physicsforums.com/attachments/164
 

Attachments

  • tring.GIF
    tring.GIF
    3.5 KB · Views: 98
Mathematics news on Phys.org
Re: Trigonometry

siyanor said:
can somebody help me out on this one,i got stuck on this one
https://www.physicsforums.com/attachments/164

That's a valid solution.

cos(3x-1) repeats every 2pi/3 so there won't be any more solutions in the domain given.
 
Re: Trigonometry

but how we are going to find the value of x ?(is my solution complete or it could go further than this?
 
Re: Trigonometry

siyanor said:
but how we are going to find the value of x ?(is my solution complete or it could go further than this?

You solved for x and it fits within the restricted domain the problem stated. You could combine the fractions but I think it's fine as it is.
 

Similar threads

MHB Solve Situational Problems Involving Trigonometric Identities
  • · Replies 3 ·
Replies
3
Views
2K
MHB Find All Trig Functions of Gamma Given cot(gamma)=4/3
  • · Replies 1 ·
Replies
1
Views
2K
High School Trigonometric Identity involving sin()+cos()
  • · Replies 11 ·
Replies
11
Views
2K
Undergrad Question ,trigonometric identities equation and functions ?
  • · Replies 4 ·
Replies
4
Views
2K
High School What values of m as a function of q satisfy this trigonometric equation?
  • · Replies 5 ·
Replies
5
Views
1K
Undergrad Getting a triangle from trigonometric function
  • · Replies 7 ·
Replies
7
Views
2K
MHB What Is the Value of $\tan^2 a + 2\tan^2 b$ Given the Trigonometric Condition?
  • · Replies 5 ·
Replies
5
Views
2K
High School Why do we need angle values greater than 90 degrees?
  • · Replies 12 ·
Replies
12
Views
4K
MHB Show the trigonometric equation has no solutions
  • · Replies 1 ·
Replies
1
Views
1K
High School Trigonometric equation -- real roots
  • · Replies 5 ·
Replies
5
Views
1K