Trigonometric equation Definition and 131 Threads

In mathematics, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involving certain functions of one or more angles. They are distinct from triangle identities, which are identities potentially involving angles but also involving side lengths or other lengths of a triangle.
These identities are useful whenever expressions involving trigonometric functions need to be simplified. An important application is the integration of non-trigonometric functions: a common technique involves first using the substitution rule with a trigonometric function, and then simplifying the resulting integral with a trigonometric identity.

View More On Wikipedia.org
Recent contents Top users
  1. Fred1230

    How to Simplify This Trigonometric Equation Using Substitutions?

    Returning if I have to show the effort, I came to this: \frac{\sin4\alpha}{1+\cos4\alpha}\cdot\frac{\cos2\alpha}{1+\cos2\alpha}\cdot\frac{\cos\alpha}{1+\cos\alpha}=\tan\frac{\alpha}{2}. =...
  2. vibha_ganji

    Help Solving a Trigonometric Equation

    I’m stuck on how to begin. I’ve tried to factor out sin theta from both of the terms on the left hand side but that led to nowhere. Could I have a hint on how to continue? Than you!
  3. brotherbobby

    Multiple angles : Reducing the sum

    Problem Statement : Let me copy and paste the problem as it appears in the text : Attempt : I haven't been able to make any significant attempt at solving this problem, am afraid. I tried to reduce all the higher submultiple angles ##2\theta, 4\theta, 8\theta## into ##\theta##, but the...
  4. chwala

    Solve the trigonometric equation below

    Solve the equation, $$cos ∅+ \sqrt 3⋅ sin ∅=1$$ in the interval, $$0≤∅≤2π$$
  5. brotherbobby

    Solving an equation for ##x## involving inverse circular functions

    Problem Statement : Solve for ##x## : Attempt : If I take ##x=\tan\theta##, the L.H.S. reads $$\tan^{-1}\frac{1-\tan\theta}{1+\tan\theta}= \tan^{-1}\left[\tan\left(\frac{\pi}{4}-\theta \right) \right ]=\frac{\pi}{4}-\theta.$$ On going back to ##x## from ##\theta##, the given equation now...
  6. P

    I Solving for ##\theta## in a Trigonometric Equation

    Can a situation at angle ##\theta## happen, where: ##d sin \theta = 3 \lambda## ##b sin \theta = 2 \lambda## ##d/b = 3/2##
  7. brotherbobby

    Trigonometric equation of two sines

    Given : The equation ##\sin m\theta + \sin n\theta = 0##. Attempt : Using the formula for ##\text{sin C + sin D}## (see Relevant Equation 3 above), the given equation simplifies to \begin{equation*} 2 \sin \frac{(m+n)\theta}{2} \cos \frac{(m-n)\theta}{2} = 0 \end{equation*} This implies the...
  8. AN630078

    Solving Reciprocal Trigonometric Equation cot^2θ+5cosecθ=4

    cot^2θ+5cosecθ=4 cot^2θ+5cosecθ-4=0 cosec^2θ+5cosec-4-1=0 cosec^2θ+5cosec-5=0 Let u=cosecθ u^2+5u-5=0 Solve using the quadratic formula; u=(-5± 3√5)/2 u=(-5+ 3√5)/2=0.8541... Substitute cosecθ=u Therefore, cosecθ=0.8541 1/sinθ=0.8541 sinθ=1/0.8541=1.170... which is not true since sin x cannot be...
  9. AN630078

    Trigonometric equation solving 2cos x=tan x

    a. I have just plotted the graph using desmos and attached an image here. Clearly, there are two values of x that satisfy the equation in the range. Do I need to add anything to this statement, I feel the response is a little brief for the question? b. Using the trigonometric identities; tan...
  10. D

    Solve the trigonometric equation involve sin(x), cos(x) and sin(x)cos(x)

    I can’t get the angle, answer given is x=56.33 , x=9.545. (All steps before the equation are correct.)
  11. PhamCy

    Trigonometry solutions Question

    Summary: https://www.physicsforums.com/threads/trigonometry-question.977263/ Here's the question. Find the solutions of the equation tan(x)=2cos(x)+1 if 0 ≤ x ≤ 2π. I know this question can be solved by observing the graph but is there any other ways (like algorithms OR some Trigonometry...
  12. D

    Solving a Trigonometric Equation: v^2*sin(180-2theta2)/g

    theta1 = 90- theta2 I substituted that into v^2*sin(2theta1)/g So I get v^2*sin(180-2theta2)/g Now I'm stuck. What do I do next?
  13. S

    Half Angle Formula for Tangent

    Hi all, I am a self learner (graduated very long ago and rusty at math) working through the Riley, Hobson and Bence text, chapter 1. 1. Homework Statement Use the fact that ##sin(\pi/6) = 1/2## to prove that ##tan(π/12) = 2 − \sqrt{3}.## Homework Equations ##tan(2x) = \frac { 2 tan(x)} {1...
  14. QuarkDecay

    Solving a trigonometric equation for the angle

    Homework Statement The equation; 0.966= -0.354sin(φ+60) + 0.935cos(φ+60) and we're trying to find φ. Homework Equations 3. The Attempt at a Solution [/B] (edited) I tried doing ^2; 0.933= 0.125sin2(φ+60) -2*0.331sin(φ+60)cos(φ+60) + 0.874cos2(φ+60) x=φ+60 0.933= 0.125sin2x - 0.331sin(2x) +...
  15. L

    B What values of m as a function of q satisfy this trigonometric equation?

    I have a trigonometric equation 2\sin \left ( \frac{q\pi }{m} \right )-\sin \left ( \frac{q\pi }{2} \right )=0 and want to know what values m as a function of q could take to satisfy the equation. Both terms zero is the obvious solution: q=2n; m=2; n is an integer. But there are more solutions...
  16. navneet9431

    Problem in finding a general solution

    Homework Statement Homework Equations General Formula for Tan(a)=Tan(b) The Attempt at a Solution See the question I have uploaded. I have tried solving it this way, Firstly I applied the Quadratic Formula to get, Now we have two cases, CASE-1 When So General Formula here will...
  17. F

    How Do You Solve sin^2(x) + tan^2(x) = √2?

    Homework Statement The problem given is sin2(x) + tan2(x) = √2 2. Homework Equations The relevant equations would be any trigonometric identities The Attempt at a Solution sin2(x) + tan2(x) = √2 sin2(x) + (sin2(x)/cos2(x) ) = √2 [ cos2(x) sin2(x) + sin2(x) ]/ cos2(x) = √2 [ (1- sin2(x))...
  18. Bobs

    Today, in our class, we received a trigonometric equation

    Today,in our class, we received a trigonometric equation ##\sin^{10}{x}+\cos^{10}{x}=\frac{29}{16}\cos^4{2x}## Here is my attempt:
  19. opus

    Isolating the Y variable in a Trigonometric Equation

    Homework Statement ##4y=cos\left(4πx+\frac{3}{2}\right)## Homework EquationsThe Attempt at a Solution In dividing both sides by 4, I got: ##y=\frac{1}{4}cos\left(πx+\frac{3}{8}\right)## But I am told this is incorrect. Not sure if dividing everything by 4 here is an allowable technique, or if...
  20. H

    What is the Sum of Angles a and b in This Trigonometry Problem?

    Homework Statement ##\sin a + \cos b## = ##\frac{-1}{2}## ##\cos a + \sin b## = ##\frac{\sqrt 3}{2}## 0 < a < ##\pi/2## ##\pi/2## < b < ##\pi## a + b = ? By calculating sin (a+b) Homework EquationsThe Attempt at a Solution I tried : ##\sin a + \cos b = 2sin\frac{(a+b)}{2}cos\frac{(a-b)}{2}...
  21. Monoxdifly

    MHB How Do You Solve tan(2x - 5) = cot(x + 5) in the Interval 0 < x < 90?

    If 0 < x < 90, what is the solution of tan(2x - 5) = cot(x + 5)? I got stuck in tan(2x - 5)tan(x + 5) = 1. What should I do after that?
  22. H

    What Are the Solutions for cos(2x) + cos(x) = 0?

    Homework Statement cos2x + cos x = 0 (0 <= x <= 360) Homework EquationsThe Attempt at a Solution cos2x + cos x = 0 2cos(3x)/2 cos(x)/2 = 0 3x/2 = 90 degrees x = 60 degrees x/2 = 90 x = 180 3x/2 = 270 x = 180 x/2 = 270 x = 540 (not qualified) is there any more possibility (answers) for x?
  23. E

    MHB Derivatives of trigonometric equation

    Could I please get help with the following question? f(x)=(2cos^2 x+3)^5/2 Any help would be very much appreciated:)
  24. CarrotWilliams

    Solving v^2/2=gs(sin(α)+cos(α)*k): Get k with Steps

    I've gotten to this point: v^2/2=gs(sin(α)+cos(α)*k) I'm suppost to get "k" from this equation can some help by showing me the steps because I'm a bit confused on how to do it.
  25. SciencyBoi

    Trigonometric inequality problem.

    Homework Statement Find the solution of the inequality ## \sqrt{5-2sin(x)}\geq6sin(x)-1 ## Answer: ## [\frac{\pi(12n-7)}{6} ,\frac{\pi(12n+1)}{6}]~~; n \in Z##Homework Equations None. The Attempt at a Solution There are two cases possible; Case-1: ##6sin(x)-1\geq0## or...
  26. M

    Finding an angle of a triangle as function of another angle

    1. Find α(β) given that the sum of the 2 sides= ##(x+y)## and its third, ##z## is a constant for 0<β<180. You can imagine that there's two pieces of string connected between two points. One string is as long as the distance between the two points while the other string is longer. If you...
  27. I

    MHB How to Solve the Trigonometric Equation 6*Sin^2(x) - 3*Sin^2(2x) + Cos^2(x) = 0?

    Good day :)! Please advise how to start with the following trigonometric equation: 6*Sin^2(x) - 3*Sin^2(2x) + Cos^2(x) = 0 To be honest, I do not know what is the first steps to start with. I have tried to start with: 5*Sin^2(x) + Sin^2(x) + Cos^2(x) - 3*Sin^2(2x) = 0 1 + 5*Sin^2(x) -...
  28. Wrichik Basu

    A problem in Inverse Circular Functions in Trigonometry

    Homework Statement :[/B] Solve for ##x ##: $$ \sin ^{-1} {x} +\sin ^{-1} {(1-x)} =\cos ^{-1} {x} $$ Answer given: ##0## or ##\frac {1}{2}##. Homework Equations :[/B] All relevant formulae on inverse circular functions may be used. The Attempt at a Solution :[/B] Please see the pic below...
  29. Wrichik Basu

    Problem in finding the General Solution of a Trigonometric Equation v3

    Homework Statement :[/B] Find the general solution of the Trigonometric equation: $$3\sin ^2 {\theta} + 7\cos ^2 {\theta} =6$$ Given andwer: ##n\pi \pm \frac {\pi}{6}## Homework Equations :[/B] These equations may help: The Attempt at a Solution :[/B] Please see the pic below: It...
  30. Wrichik Basu

    Problem in finding the General Solution of a Trigonometric Equation v2

    Homework Statement :[/B] Find the general solution of the equation: $$\tan {x}+\tan {2x}+\tan {3x}=0$$ Answer given: ##x=## ##\frac {n\pi}{3}##, ##n\pi \pm \alpha## where ##\tan {\alpha} = \frac {1}{\sqrt {2}}##. Homework Equations :[/B] These equations may be used: The Attempt at a...
  31. Wrichik Basu

    A problem in finding the General Solution of a Trigonometric Equation

    Homework Statement :[/B] Find the general solution of the Trigonometric equation $$\sin {3x}+\sin {x}=\cos {6x}+\cos {4x} $$ Answers given are: ##(2n+1)\frac {\pi}{2}##, ##(4n+1)\frac {\pi}{14}## and ##(4n-1)\frac {\pi}{6}##. Homework Equations :[/B] Equations that may be used: The...
  32. M

    B Trigonometric equation -- real roots

    The number of real roots of the equation $$2cos \left( \frac {x^2 + x} {6} \right)=2^x + 2^{-x}$$ Answer options are : 0,1,2,∞ My approach : range of cos function is [-1,1] thus the RHS of the equation belongs to [-2,2] So, we have -2 ≤ 2x + 2-x ≤ 2 solving the right inequality, i got 2x...
  33. D

    Solve acos²θ+bsinθ+c=0 for all values 0≤θ≤360°

    Homework Statement Solve acos²θ+bsinθ+c=0 for all values 0≤θ≤360° a=16 b=6 c=-12 So 16cos²θ+6sinθ-12=0 Homework Equations Cos²x=1-Sin²x The Attempt at a Solution Identity: Cos²x=1-Sin²x 16(1-Sin²θ)+6Sinθ-12=0 16-16Sin²θ+6Sinθ-12=0 6Sinθ-16Sin²θ=12-16=-4 Divide by 2(?) 3Sinθ-8Sin²θ=-2...
  34. FritoTaco

    Solving a Trigonometric Equation

    Homework Statement Find all solutions of the equation in the interval [0, 2\pi]. sin6x+sin2x=0 Homework Equations Double Angle Formulas sin2x=2sinxcosx cos2x=cos^{2}x-sin^{2}x =2cos^{2}x-1 =1-2sin^{2}x (3 formulas for cos2x) tan2x=\dfrac{2tanx}{1-tan^{2}x} Sum to Product Formula...
  35. L

    MHB How can I solve the trigonometric equation $(2-\sqrt{2})(1+\cos x)+\tan x=0$?

    Hi, I've tried to solve this equation: $(2-\sqrt{2})(1+\cos x)+\tan x=0$ and I've tried everything but nothing works...Does anybody have an idea?
  36. teetar

    Solving trigonometric equation of a sum of unknowns

    Homework Statement \sin (x) = \frac{2}{3} and \sec (y) = \frac{5}{4}, where x and y lie between 0 and \frac{\pi}{2} evaluate \sin (x + y) Homework Equations Looked over some trig laws, don't think I saw anything that's too relevant. There \sec (x) = \frac{1}{\sin (x)} The Attempt at a...
  37. Alettix

    Trigonometric Equation Solving: Cosine and Sine Identities for Homework

    Homework Statement The following equation is to be solved for all x: ## \cos(x) + \cos(3x) = \sin(x) + \sin(3x)## Homework Equations The tripple angle formulas: ## \cos(3x) = 4\cos^3(x) - 3\cos(x) ## ##\sin(3x) = 3\sin(x) - 4\sin^3(x) ## The Pythagorean trig identity: ## \sin^2(x) + \cos^2(x)...
  38. I

    MHB Solve the trigonometric equation sin(2theta-pi/6) = cos(2theta)

    i need help with question 4a. Thank to anyone who helped.
  39. N

    MHB Can You Determine the Value of A When B Equals 4 in a Trigonometric Equation?

    A=3sinx+4cosx and B=3cosx-4sinx if B = 4 find A. What i tried is to use 4=3cosx-4sinx and solve for cosx now cosx = (4+4sinx)/3 plug this into A I end up getting A = (25sinx+16)/3 am I correct?
  40. F

    Trigonometric equation for stress

    Homework Statement is the circled part wrong ? Homework EquationsThe Attempt at a Solution how could 0.5 sin2theta = ( 1 + cos2theta ) / 2 ?
  41. 9

    Differentiate trigonometric equation

    Homework Statement a) Differentiate the following equation with respect to: 1) θ 2) Φ 3) ψ (Ua - Ub)' * C * r where: C is a 3 x 3 rotation matrix: [ cos θ cos ψ, -cos Φ sin ψ + sin Φ sin θ cos ψ, sin Φ sin ψ + cos Φ sin θ cos ψ] [ cos θ sin ψ, cos Φ cos ψ + sin Φ sin θ sin...
  42. D

    Solution to this trigonometric equation

    Homework Statement ##tanx=\frac{(1+tan1)(1+tan2)-2}{(1-tan1)(1-tan2)-2}## find x Homework Equations 3. The Attempt at a Solution [/B] I tried multiplying through the paranthesis and arrived at ##tanx=\frac{(tan1tan2-1)+(tan2+tan1)}{(tan1tan2-1)-(tan2+tan1)}## and i don't know if this is any...
  43. P

    Finding sum of roots of trigonometric equation

    Homework Statement Question: Sum of all the solutions of the equation: ##tan^2 (33x) = cos(2x)-1## which lie in the interval ## [0, 314] ## is: (a) 5050 π (b) 4950 π (c) 5151 π (d) none of these The correct answer is: (b) 4950 π Homework Equations ## cos(2x) = 2cos^2(x) -1 ## The Attempt...
  44. A

    Trigonometric equation sin(x) = C*sin(y)

    Homework Statement sin x = C*sin y Find y as a function of x for a given C>0. Homework Equations sin x = C*sin y The Attempt at a Solution This is not actually a problem from a book, but a problem I myself thought about. I was studying elastic collisions in SCM and I obtained 2 equations...
  45. MironeDagains

    Solve Trig Equation with 2 & -Π/6 Inside Brackets

    http://www5a.wolframalpha.com/Calculate/MSP/MSP238521i5b83i951f19c3000010ca05be63f0bfc0?MSPStoreType=image/gif&s=10&w=219.&h=85. How do I solve this? I know the answers, as Wolphram Alpha has given me only the answers without any steps to how they derived those answers. I know that sin(x)=√3/2...
  46. anemone

    MHB Can You Solve This Trigonometric Equation for $x$?

    Solve for $x$ such that $2\sin(x+30^\circ)\sin 16^\circ \sin 76^\circ=\sin 2028^\circ \sin 210^\circ$ for $0\lt x \lt 180^\circ$.
  47. M

    MHB How to Solve Trigonometric Equation sin2x = sqrt(2)/2 Using Algebra?

    Solve sin2x= sqrt(2)/2 (using algebra) the interval is between 0 and 2pi i got the first two answers: pi/8 and 3pi/8, but i don t understand how to get the other two: 9pi/8 and 11pi/8. thanks!
  48. M

    Transforming Trigonometric Equation

    Homework Statement In 2001, Windsor, Ontario received its maximum amount of sunlight, 15.28 hrs, on June 21, and its least amount of sunlight, 9.08 hrs, on December 21 Due to the Earth's revolution about the sun, the hours of daylight function is periodic. Determine an equation that can...
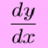
  49. iwantcalculus

    Questions on Trigonometric equation solving

    Hello reader, I have an exam really soon and it includes a good bit of trigonometry, but I'm having problems with the trig stuff because this exam does not allow calculators and since I was dependent on the calculator, I haven't memorized anything about the trigonometric functions. I don't know...
  50. W

    MHB Find the Smallest Angle for sin theta+5cos theta=4 | Trigonometric Equation Help

    Can anyone help with this trig question, Determine the smallest angle in degrees such that sin theta+5cos theta=4 Iknow i need to use the quadratic formula but really stuck on it.
Back
Top