alex740rider
- 8
- 0
I've been stuck on part b for several hours now (feels like the whole day).
1. Homework Statement :
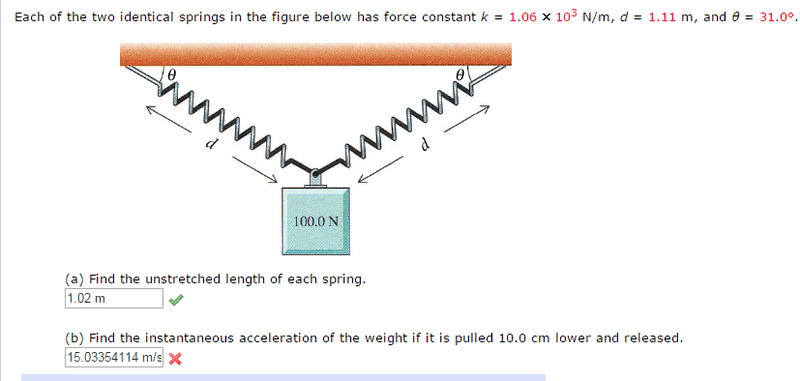
2. Homework Equations :
2 k * x sin(θ') = 100/g * a
sum(Fy) = F net
Ma = 2kxsin(angle) - 100
a = (2kxsin(angle) - 100) / (100 / 9.8)
2*kxsin(θ')-100 / 10.2
3. The Attempt at a Solution :
What I've done so far...
x component of d = d cos(θ) = 1.11 cos(31)= 0.95 (.9514557038)
y component of d = d sin(θ) = 1.11 sin(31) = 0.57 (.5716922632)
added 10 cm to y component = 0.67 (.6716922632)
θ' =tan-1( 0.67 / 0.95)
θ' = 35.19° (35.22066645)
d' = sqrt((x component of d)^2 + (New y component of d) ^2 )
d' = sqrt(0.95^2 + 0.67^2) (1.164662377)
d’ = 1.164662377
x= d' - Unstretched length of spring
x = 1.164662377 - 1.02
x = 0.1446623771 m
exact values (for those wondering):
< = 35.22069645
d' = 1.164662377
mg = 100N
m = 100/g
I used 2 k * x sin(θ') = 100/g * a
And plugged in 2*1060*0.1446623771*sin(35.22069645)*9.8/100 and got 17.33356261 m/s^2 ;and it's still incorrect...
I also tried another equation
Ma = 2kxsin(angle) - 100
a = (2kxsin(angle) - 100) / (100 / 9.8)
a = 2*1060*0.1446623771*sin(35.22069645) - 100 / 100/9.8
a = 7.533575457 m/s^2
^(still incorrect)
currently at 71/100 for attempts...
So far, I've slumped 3 tutors on Cheggs, math majors, physics major, you name it. And yes I have tried contacting the teacher for the past few days, no replies back yet. This is starting to be very frustrating.
god bless
p.s.; this is how I got part a:
2*1060*sin(31) = 1091.880719
100/1091.880719 = .0915850956
1.11-.0915850956 = 1.018414904
I rounded it to 1.02 and got it right on webassign (not sure if it made a difference)
1. Homework Statement :
2. Homework Equations :
2 k * x sin(θ') = 100/g * a
sum(Fy) = F net
Ma = 2kxsin(angle) - 100
a = (2kxsin(angle) - 100) / (100 / 9.8)
2*kxsin(θ')-100 / 10.2
3. The Attempt at a Solution :
What I've done so far...
x component of d = d cos(θ) = 1.11 cos(31)= 0.95 (.9514557038)
y component of d = d sin(θ) = 1.11 sin(31) = 0.57 (.5716922632)
added 10 cm to y component = 0.67 (.6716922632)
θ' =tan-1( 0.67 / 0.95)
θ' = 35.19° (35.22066645)
d' = sqrt((x component of d)^2 + (New y component of d) ^2 )
d' = sqrt(0.95^2 + 0.67^2) (1.164662377)
d’ = 1.164662377
x= d' - Unstretched length of spring
x = 1.164662377 - 1.02
x = 0.1446623771 m
exact values (for those wondering):
< = 35.22069645
d' = 1.164662377
mg = 100N
m = 100/g
I used 2 k * x sin(θ') = 100/g * a
And plugged in 2*1060*0.1446623771*sin(35.22069645)*9.8/100 and got 17.33356261 m/s^2 ;and it's still incorrect...
I also tried another equation
Ma = 2kxsin(angle) - 100
a = (2kxsin(angle) - 100) / (100 / 9.8)
a = 2*1060*0.1446623771*sin(35.22069645) - 100 / 100/9.8
a = 7.533575457 m/s^2
^(still incorrect)
currently at 71/100 for attempts...
So far, I've slumped 3 tutors on Cheggs, math majors, physics major, you name it. And yes I have tried contacting the teacher for the past few days, no replies back yet. This is starting to be very frustrating.
god bless
p.s.; this is how I got part a:
2*1060*sin(31) = 1091.880719
100/1091.880719 = .0915850956
1.11-.0915850956 = 1.018414904
I rounded it to 1.02 and got it right on webassign (not sure if it made a difference)
Last edited: