Discussion Overview
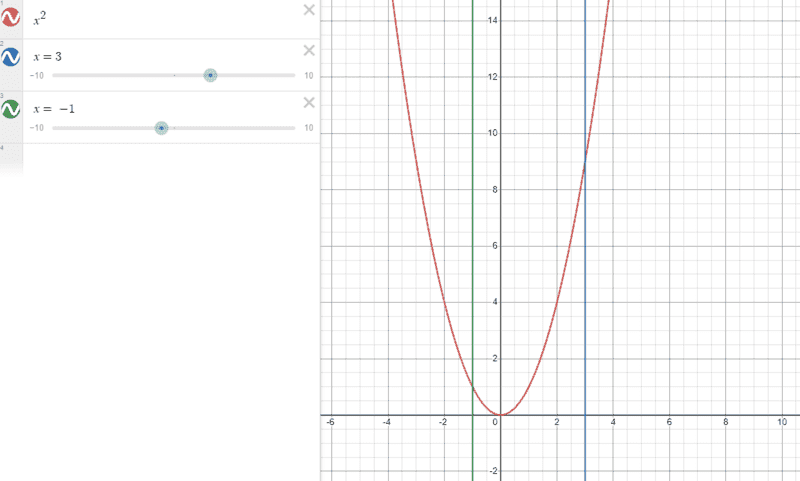
The discussion revolves around the interpretation of definite integrals, specifically addressing the calculation of area under the curve of the function \(x^2\) from \(x = 3\) to \(x = -1\). Participants explore the implications of the integral's limits and the concept of oriented areas in calculus.
Discussion Character
- Technical explanation
- Conceptual clarification
- Debate/contested
Main Points Raised
- One participant calculates the integral \(\int_3^{-1} x^2 \, dx\) and finds it to be negative, questioning why the area is negative when the graph shows it is above the x-axis.
- Another participant explains that integrals represent oriented areas, noting that reversing the limits of integration changes the sign of the result.
- A subsequent reply suggests that a negative integral implies negative area, prompting further questioning about the nature of area above the x-axis.
- Another participant corrects the interpretation, stating that the limits of integration were in the wrong order, and that the integral should be calculated from left to right to yield a positive value.
- Further elaboration is provided on the distinction between the value of an integral and the concept of area, emphasizing that areas are always positive while integrals can be negative depending on the orientation and limits.
- An example involving the sine function is presented to illustrate that while the integral can be zero, the area under the curve is not, reinforcing the difference between area and integral values.
Areas of Agreement / Disagreement
Participants express differing views on the interpretation of negative integrals and their relation to area, with some asserting that areas must be positive while others explore the implications of negative integral values. The discussion remains unresolved regarding the broader implications of these concepts.
Contextual Notes
Participants highlight the importance of the order of limits in integration and the distinction between area and integral values, indicating that misunderstandings can arise from these factors. The discussion does not resolve the conceptual nuances surrounding these topics.