Mike_bb
- 191
- 19
Hello.
As is known, we can neglect high-order term in expression ##f(x+dx)-f(x)##. For ##y=x^2##: ##dy=2xdx+dx^2##, ##dy=2xdx##.
I read that infinitesimals have property: ##dx+dx^2=dx##
I tried to neglect high-order terms in integral sum (##dx^2## and ##4dx^2## and so on) and I obtained wrong result in the end.
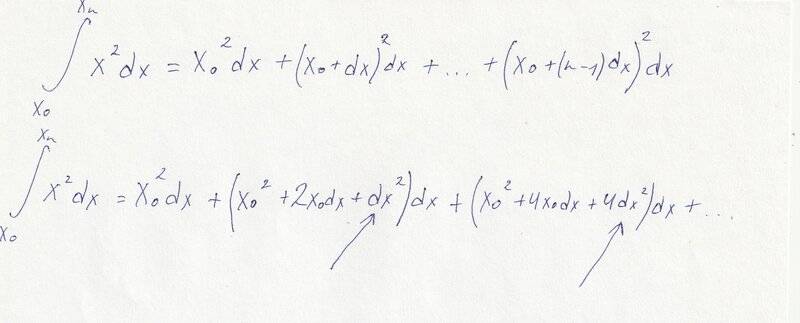
Where is my mistake?
Thanks.
As is known, we can neglect high-order term in expression ##f(x+dx)-f(x)##. For ##y=x^2##: ##dy=2xdx+dx^2##, ##dy=2xdx##.
I read that infinitesimals have property: ##dx+dx^2=dx##
I tried to neglect high-order terms in integral sum (##dx^2## and ##4dx^2## and so on) and I obtained wrong result in the end.
Where is my mistake?
Thanks.