Net efficiency of a cascaded Carnot Engine and Fridge

[baseballfan_ny]

Homework Statement

The efficiency of a heat engine is to be improved by lowering the temperature of its low temperature reservoir to a value $T_r$, below the environmental temperature $T_l$ by means of a refrigerator. The refrigerator consumes part of the work produced by the heat engine. Assume that both the heat engine and the refrigerator operate reversibly. Calculate the ratio of the net (available) work to the heat $Q_h$ supplied by the heat equation at temperature $T_h$. Is it possible to obtain a higher net conversion energy efficiency this way?

Relevant Equations

$$ S_{in} = \frac { Q_{in} } { T_{in} } = S_{out} = \frac { Q_{out} } { T_{out} } $$
$$W_{engine} = Q_{in} - Q_{out}$$
$$W_{fridge} = Q_{out} - Q_{in}$$

Here is a diagram of my interpretation of the problem:

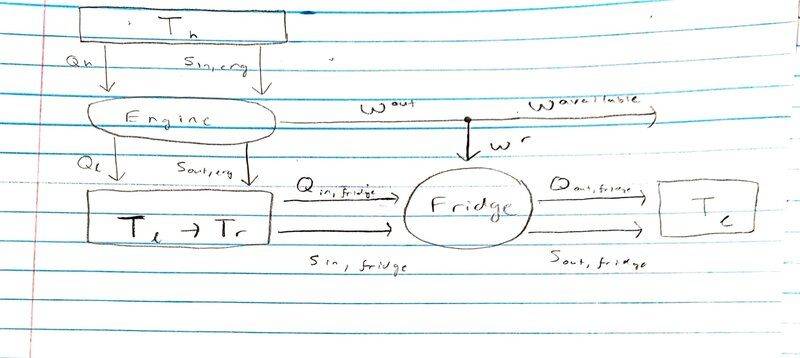
Where I'm thinking that the engine originally takes heat from $T_h$ to $T_l$, in which case $\frac { Q_{h} } { T_{h} } = \frac { Q_{l} } { T_{l} }$ and $W_{out} = Q_{in} - Q_{out} = Q_h \left( 1 - \frac {T_l} {T_h} \right)$.

Then I suppose that because $T_l$ is cooled to $T_r$, I get $W_{out} = Q_h \left( 1 - \frac {T_r} {T_h} \right)$.

The fridge itself consumes a certain amount of work $W_r = Q_{out, fridge} - Q_{in, fridge}$. And because $\frac { Q_{in, fridge} } { T_{r} } = \frac { Q_{out, fridge} } { T_{l} }$ so I can write $W_r = Q_{in, fridge} \left( \frac {T_l} {T_r} - 1 \right)$.

And now just trying to get $$ \frac {W^{available} } {Q_h} = \frac {W_{out} - W_r } {Q_h} = \frac { Q_h \left(1 - \frac {T_r} {T_h} \right) - Q_{in, fridge} \left( \frac {T_l} {T_r} - 1 \right) } {Q_h}$$.

But my problem is that I don't know what $Q_{in, fridge}$ is. An optimistic guess I have is that $Q_{in, fridge} = Q_l$ by sort of applying energy conservation to the reservoir the same way we did to the engines and fridges to get the work delivered or work consumed, but I'm not sure that works that easily in the case of a reservoir? Thanks in advance for the feedback.

 

[TSny]

So far, your work looks good to me. And I also interpret the problem as implying that we should assume $Q_{in, fridge} = Q_l$. That way, whatever heat is dumped into the cold reservoir at temperature $T_r$ by the heat engine is removed from the cold reservoir by the fridge and dumped into the environment. So, the cold reservoir can maintain a steady temperature even if the cold reservoir is not huge. Also, the assumption that $Q_{in, fridge} = Q_l$ leads to an interesting result for $\large \frac{W^{available}}{Q_h}$.