rajeshmarndi
- 319
- 0
Homework Statement
There is a point P(x,y) and now I rotate the x-y axis, say by θ degree. What will be the coordinates of P from this new axis.
I have google but found formula for new coordinates when the points is rotated by θ degree. So I tried my own. So is there other simplified formula for the above situation.
Homework Equations
The Attempt at a Solution
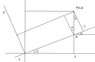
Plz see the attached figure.
AC-AD is the new axis and (x',y') are the new coordinates of point P.
y'=PC
cos θ= PC/PB = y'/PB
y'= PB cos θ
PB= y- BE
tan θ= BE/x , BE = x tanθ
PB = y - xtanθ
y'= (y- xtanθ) cosθ
= ycosθ - xsinθ --------------eq(1)x'= AB + BC
sinθ=BE/AB
AB=BE/sinθ, tanθ=BE/x
BE=xtanθ
AB=xtanθ/sinθ = x/cosθ
tanθ = BC/y'
BC= y'tanθ
= (ycosθ-xsinθ)tanθ , ( y' from eq(1) )
= ysinθ - x sinθtanθ
x' = AB + BC
= x/cosθ + ysinθ - x sinθtanθ
So the new coordinates are
x'= x/cosθ + ysinθ - x sinθtanθ
y'= ycosθ - xsinθ