so_gr_lo
- 69
- 10
- Homework Statement
- A balloon has nm moles of monatomic ideal gas in thermal equilibrium with outside air at temperature T1. The pressure inside is P1+ delta. The ambient temperature increases isobarically from T1 to T2. The pressure then drops to P2 causing it to expand adiabatically until it’s temperature is again T1. Show that the new volume of the gas is (result shown in solution)
I seem to get T1 and T2 the wrong way round but can’t see how to fix it
- Relevant Equations
- T1V1^(y-1) = T2V2^(y-1)
P1V1^y = P2V2^y
Result

My attempt
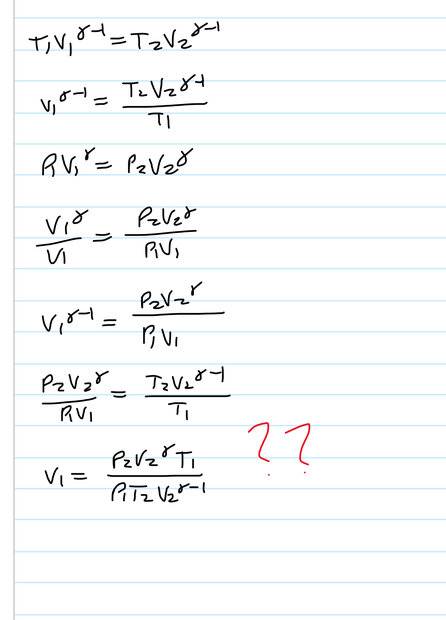
My attempt