Newton's Laws o motions - two wedges - one sliding over the other

[dharavsolanki]

Homework Statement

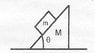
A block of mass m lies on a wedge of mass M as shown in figure. Answer the following parts separately.

(a) - With what minimum acceleration must the wedge be moved towards right horizontally so that the block m falls freely?
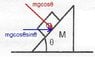
(b) - Find the minimum friction co-efficient required between M and ground so that it does not move while block m slips down on it.

Variables - Mu(ground), a_m and a_M

Homework Equations

F = ma

The Attempt at a Solution

Not able to start anything anywhere.

For (a)
- - - - -
I can't make equations out of the situation, but I am getting a weird feeling it is the same thing as a satellite. It keeps on falling towards the earth, only that the Earth keeps on receding. The only difference being that the falling object not reaching the ground was "Earth's curvature" in one case and "Slope of wedge" in the other. Not sure how to translate this idea into equations.

For (b)
- - - - -
I have attempted it, but it gets too complicated, the normal reaction between the two wedges changes the normal reaction between the surfaces and such. How should I carry on with this?

 

[method_man]

I don't know if this will help you. I have attached a picture. Block m acts on the wedge with force mgcosΘ. So, when the wedge starts moving to the right with acceleration a, you have got two forces acting in horizontal direction:
mgcosΘsinΘ=(m+M)a.

When you have got the friction:
mgcosΘsinΘ=(m+M)μ

 

[dharavsolanki]

I don't know if this will help you. I have attached a picture. Block m acts on the wedge with force mgcosΘ. So, when the wedge starts moving to the right with acceleration a, you have got two forces acting in horizontal direction:
mgcosΘsinΘ=(m+M)a.

When you have got the friction:
mgcosΘsinΘ=(m+M)μ

Why have you taken (m + M) as the system both the times? Both of them are independent blocks and their motions have no relations. Plus, since the two blocks are accelerated, the normal reaction between the two blocks would be zero. Hence, between the ground and the inclined plane, the normal reaction is not (m + M)g.

The points that confuse me are these.

Can you please post the equations from where I can start?

 

[rl.bhat]

Forces acting on the block are
mgsinθ------- along the inclined plane
mgcosθ--------perpendicular to the inclined plane, and
N -----normal reaction due to the wedge.
Wedge is moving towards right. When it moves through a distance x, to keep in touch with wedge, block moves through a distance y in the direction perpendicular to the wedge.
And y = x*sinθ. Οr ay = a*sinθ where a is the acceleration of the wedge.
For the block
m*ay = mg*cosθ - Ν. For the free fall of the block, N should be equal to zero.
Now put the value of ay in the above equation to find the acceleration.
Similarly find the forces acting on the wedge and find the acceleration when the block is slipping. Calculate the frictional force which can prevent this motion.