pinsky
- 95
- 0
I'm having some problems in observing the total force which.
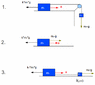
The original situation is numbered "1."
There is a resultant force F_r = m_2 \cdot g - k \cdot m_1 \cdot g
and because of that force m1 has the acceleration a.
What I can't seem to figure out is is that resultant force equal.
F_r = m_1 \cdot a
or
F_r = (m_1 + m_2) \cdot a
In defense of the first argument, I've drawn the equivalent picture (2.) in which the second mass is replaced just by the force it exerts to m1.
In that case, it is clear that the first equation for Fr is the correct one.
But, I've also drawn a second equivalence for which the second equation would make more sense.
I know that one of them is wrong, i just can't seem to figure out which :)