No. of solutions of an equation involving a defined function

[Physics lover]

Homework Statement

The number of solutions of the equation
$f(x-1)+f(x+1)=sinA ,0<A<\pi/2$
where
$f(x)$={$1-|x|,|x|$ less than or equal to 1
={$0,|x|>1$
is

Relevant Equations

None

Here is a pic of question

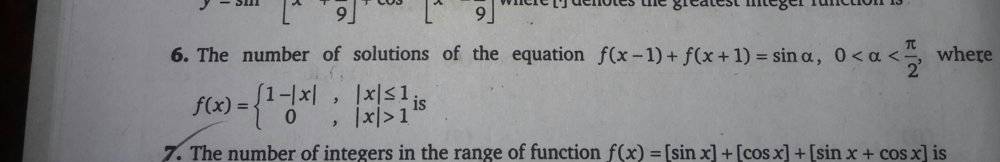
My attempt-:
I defined functions f(x-1) and f(x+1) using f(x).After defining them,I substituted their values in the equation f(x-1)+f(x+1)=sinA.
For different ranges of x,I got different equations.
For 1<x<2,I got 1-x=sinA.
But now I am confused.For each different value of x in the interval (0,1],there exists an A.So there would be infinite solution.But the answer was given as 4.
Please help..

 

[haruspex]

For each different value of x in the interval (0,1],there exists an A.

I would think they want the number of solutions for any given fixed A in the range, though why they go through a sin function instead of just giving a range 0<…<1 I don't know.

 

[Physics lover]

I would think they want the number of solutions for any given fixed A in the range, though why they go through a sin function instead of just giving a range 0<…<1 I don't know.

Yes i think the same.Maybe the question is incorrect.

 

[haruspex]

Yes i think the same.Maybe the question is incorrect.

No, with my interpretation I get the book answer, so you might as well assume that is what is intended.

 

[Physics lover]

No, with my interpretation I get the book answer, so you might as well assume that is what is intended.

So shall I put any value of A in between 0 and pi/2?

 

[haruspex]

So shall I put any value of A in between 0 and pi/2?

No, you have to show that for every A in that range there are four solutions for x.
If you sketch f(x+1)+f(x-1) it will be obvious.

 

[Physics lover]

No, you have to show that for every A in that range there are four solutions for x.
If you sketch f(x+1)+f(x-1) it will be obvious.

Yes I got it.Thanks.