Non-Differentiable Function proof

[ChiralSuperfields]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

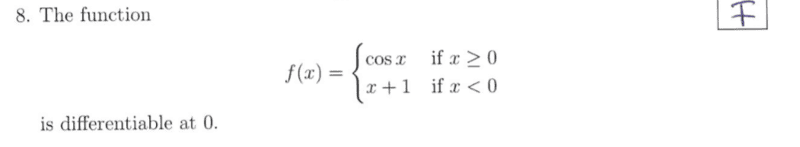
I am trying to prove that this function is non-differentiable at 0.

In order for a function to be non-differentiable at zero, then the derivative must not exist at zero $⇔ \lim_{x \to 0} \frac{f(x) - f(0)}{x - 0}$ does not exist or $⇔ \lim_{x \to 0^-} \frac{f(x) - f(0)}{x - 0} \neq \lim_{x \to 0^+} \frac{f(x) - f(0)}{x - 0}$

$\lim_{x \to 0^-} \frac{f(x) - f(0)}{x - 0} = \lim_{x \to 0^-} \frac{x + 1 - 1}{x} = 1$

$\lim_{x \to 0^+} \frac{\cos x - \cos 0}{x} = \lim_{x \to 0^+} \frac{\cos x - 1}{x}$ Howver, I'm not sure where to go from here.

Does someone please know?

Thanks!

 

[Hill]

Hint: $\cos x \leq 1$.

 

[Orodruin]

Both numerator and denominator in your last limit approach zero. Use the l'Hopital rule!

Hint: $\cos x \leq 1$.

This does not really help finding the correct limit. $1-x$ is also $\leq 1$ for $x > 0$ and gives a different limit than $\cos(x)$.

 

[Hill]

This does not really help finding the correct limit.

Of course it does not, but the OP does not need it. It only needs to show that this limit is not $1$.

 

[docnet]

Hey OP. The proof rests on the fact that if the left sided and right sided limits at $x=0$ aren't equal, then the limit at $x=0$ is undefined. You're almost there, just a bit more work is needed.

 

[Orodruin]

Of course it does not, but the OP does not need it. It only needs to show that this limit is not $1$.

This is true, but not that much easier than to actually compute the limit using the l'Hopital rule.

 

[Office_Shredder]

This is true, but not that much easier than to actually compute the limit using the l'Hopital rule.

I find it a bit weird to suggest someone compute the derivative of cos(x) as a substep in their struggle to compute the derivative of cos(x). I don't think the suggestion is really that appropriate - either we know the derivative of cos(x) is sin(x) and we should use that fact directly, or we should do some other analysis on the limit that doesn't involve differentiation. I'll let op opine on whether they have learned the derivative of cos(x) yet

 

[Orodruin]

I find it a bit weird to suggest someone compute the derivative of cos(x) as a substep in their struggle to compute the derivative of cos(x). I don't think the suggestion is really that appropriate - either we know the derivative of cos(x) is sin(x) and we should use that fact directly, or we should do some other analysis on the limit that doesn't involve differentiation. I'll let op opine on whether they have learned the derivative of cos(x) yet

This is true. Brain fart on my part. I guess I just looked at the last limit without reading the rest ...

To compute the derivative I would then apply either the derivative of $e^{ix}$, which should be known to be $i e^{ix}$ or use the series definition of the cosine from which it should be clear that $\cos(x) = 1 - x^2/2 + \mathcal O(x^4)$, which is sufficient to get the result.

 

[nuuskur]

$\lim_{x \to 0^+} \frac{\cos x - 1}{x}$ Howver, I'm not sure where to go from here.

Recall that $2\sin^2x = 1-\cos 2x$ and consider the behaviour of $\frac{\sin t}{t}$ as $t\to 0$.