Non-dimensionalization of the energy balance

[MexChemE]

Good evening people of PF! I have recently encountered a problem from Himmelblau's Basic Principles and Calculations in Chem. E. which asks to set up an energy balance for a tank, and then non-dimensionalize the differential equation before solving it. It's not the most complex task, but it's the first time I've done it and I wanted to know if I did things right. Here's an sketch of the system.

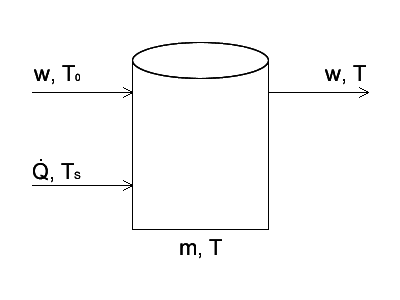
Mass flows in and out at the same rate w, therefore the mass inside the tank is a constant, m. Heat is being transferred into the contents of the tank using a coiled tube heater, in which steam flows at temperature T_S. The rate of heat transfer is given by $\dot{Q} = hA(T_S - T)$. Fluid entering the tank has a constant temperature of T₀, which is also the temperature of the system at t = 0. The differential energy balance for the system is
$$\frac{\textrm{d} U}{\textrm{d} t} = \dot{Q} - w \Delta H$$
In terms of temperature
$$m C_p \frac{\textrm{d} T}{\textrm{d} t} = hA(T_S - T) - w C_p (T-T_0)$$
The problem only tells you the non-dimensional parameters you are supposed to use
$$\Theta = \frac{T-T_0}{T_S - T_0}$$
$$\tau = \frac{w}{m} t$$
$$\beta = \frac{hA}{w C_p}$$
Which are temperature, time, and an additional constant parameter. In order to start scaling the equation I decided to divide the entire equation by wC_p(T_S-T₀). Also, I've seen some heat transfer textbooks use the relation dT = d(T-T₀), because T₀ is a constant, so I decided to apply said relation and ended up with the following equation
$$\frac{m C_p}{w C_p} \frac{\textrm{d}}{\textrm{d} t} \left( \frac{T-T_0}{T_S-T_0} \right) = \frac{hA(T_S - T)}{w C_p (T_S - T_0)} - \frac{w C_p (T-T_0)}{w C_p (T_S - T_0)}$$
$$\frac{m}{w} \frac{1}{\frac{m}{w}} \frac{\textrm{d} \Theta}{\textrm{d} \tau} = \beta \frac{T_S - T}{T_S - T_0} - \Theta$$
Using
$$\frac{T_S - T}{T_S - T_0} = 1 - \Theta$$
We get the non-dimensionalized energy balance
$$\frac{\textrm{d} \Theta}{\textrm{d} \tau} = \beta (1- \Theta) - \Theta$$
$$\frac{\textrm{d} \Theta}{\textrm{d} \tau} = \beta - (\beta +1) \Theta$$

In my opinion, it is not necessary to non-dimensionalize the original D.E. in order to solve it, however, I guess it's a good training problem for non-dimensionalization. I was hoping it could get some insights about how to perform the non-dimensionalization procedure more efficiently. Also, I was wondering, if one is not given the non-dimensional parameters to use, is there a set of rules for choosing them or is it just common sense and practice?

Thanks in advance for any input!

 

[Chestermiller]

Hi MexChemE,

Yes, there is a rational methodology for arriving at the dimensionless parameters to use. I'm sure you will learn about that soon. I feel that you did just fine in doing the de-dimensionalization using the parameters that you were given. You will also very soon learn how powerful a tool de-dimensionalization is, since all physical phenomena really operate in terms of dimensionless groups. Also, if you can reduce a problem having 10 dimensional parameters to one that has only 3 dimensionless parameters, I'm sure you will agree that there is great value in that. Then, when you are modeling the behavior and you want to find out the effect of changing the operating parameters, you don't need to vary 10 things independently, you only need to vary 3. Presenting results graphically is also made greatly simplified when there are fewer parameters needed on the graph.

Chet

 

[MexChemE]

You will also very soon learn how powerful a tool de-dimensionalization is, since all physical phenomena really operate in terms of dimensionless groups. Also, if you can reduce a problem having 10 dimensional parameters to one that has only 3 dimensionless parameters, I'm sure you will agree that there is great value in that. Then, when you are modeling the behavior and you want to find out the effect of changing the operating parameters, you don't need to vary 10 things independently, you only need to vary 3. Presenting results graphically is also made greatly simplified when there are fewer parameters needed on the graph.

Hi Chet. I did find the procedure quite entertaining. And I agree with what you say, once I start working with dimensionless numbers groups I will realize the real usefulness of non-dimensionalization. So far, I like the fact that dimensionless temperature can only take values from 0 to 1 and represents how close you are to the steam temperature. While reading about it, I did notice some similarities of the β parameter with some sort of product of the Biot and Fourier numbers, however, they were not exactly the same. I'll see what I can learn about it from BSL.

I will proceed to graph the equation in Excel and vary some of the parameters to see if I can gain some extra insights from the graphical analysis. Maybe I'll even compare the graphical analyses of the regular and dimensionless models and try to establish pros and cons for each one.

Thanks!

 

[Chestermiller]

Hi Chet. I did find the procedure quite entertaining. And I agree with what you say, once I start working with dimensionless numbers groups I will realize the real usefulness of non-dimensionalization. So far, I like the fact that dimensionless temperature can only take values from 0 to 1 and represents how close you are to the steam temperature. While reading about it, I did notice some similarities of the β parameter with some sort of product of the Biot and Fourier numbers, however, they were not exactly the same. I'll see what I can learn about it from BSL.

I will proceed to graph the equation in Excel and vary some of the parameters to see if I can gain some extra insights from the graphical analysis. Maybe I'll even compare the graphical analyses of the regular and dimensionless models and try to establish pros and cons for each one.

Thanks!

Plot Θ vs τ at various values of β, and be done with it. Also, your β parameter occurs in many problems.

Chet