Normal Force and Coefficient of Kinetic Friction

[gcombina]

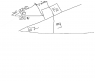
A 250-N force is directed horizontally as shown to push a 29-kg box up an inclined plane at a constant speed. Determine the magnitude of the normal force, FN, and the coefficient of kinetic friction, µk.
So, I know I have to find the vertical and parallel forces
Vertical: Fn and 250 sin of angle (where is the angle symbol?)

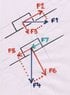
so, if you look at the second picture, that is where I get stucked. Is "mg" also part of the parallel force?

 

[dean barry]

I think your normal force vector from the push force is upside down.
Split the weight of the block ( m * g ) into its parallel and normal vectors

 

[gcombina]

Thank you but I don't understand, what do you mean is upside down?

 

[dean barry]

Its easier if i sketch something up, ill get back to you.

 

[nasu]

Thank you but I don't understand, what do you mean is upside down?

The normal component of the pushing force is towards the plane. It's pushing the block against the incline, not trying to lift it from it.
Your arrow shows otherwise.

 

[dean barry]

heres that sketch, the upper shows the force resolution for the 250 N pushing force ( F1 )
F2 = F1 * cosine 27 °
F3 = F1 * sine 27 °
The lower shows the force resolution for the force of the block ( m * g ) F4
F5 = F4 * sine 27 °
F6 = F4 * cosine 27 °
F7 is the friction force and = ( F6 + F3 ) * µ
( µ = friction co-efficient )

Note : if the velocity is constant, forces up the slope = forces down the slope

 

[gcombina]

thanks, let me study this. I just came back to the thread

 

[gcombina]

sorry but this confuses me more

 

[CWatters]

Which bit is confusing?

The 250N force acts towards the slope. The component that contributes to the normal force is F3
Gravity acts towards the slope. The component that contributes to the normal force is F6

The sum of (F3+F6) also act towards the slope.

You appear to be trying to make the trig show the sum pointing away from the slope? Perhaps you are confused because the normal force FN is usually shown as the equal and opposite reaction that ground makes on the block?

 

[gcombina]

http://Newton.physics.uiowa.edu/~rmerlino/11Sum13/11Smr13_E2_Practice.pdf

I am following this and it looks different.

Looking at the x-forces, can you tell me why this person does

mg sin 27 - Fcos angle + Fk? I don't understand the signs by looking at his graphic

 

[haruspex]

http://Newton.physics.uiowa.edu/~rmerlino/11Sum13/11Smr13_E2_Practice.pdf

I am following this and it looks different.

Looking at the x-forces, can you tell me why this person does

mg sin 27 - Fcos angle + Fk? I don't understand the signs by looking at his graphic

Because the first and third terms both act down the plane (positive x), while the second term acts up the plane.

 

[CWatters]

What Haruspex said.

With reference to Deans drawings and taking down the slope as positive..

mg sin 27 - Fcos angle + Fk = 0

translates as

F5 - F2 + F7 = 0

or you could instead take up the slope as positive, in which case that would be

-F5 + F3 - F7 = 0

 

[dean barry]

Why don't you work a fresh problem through first, (to get the feel) try this one :
A cannonball is launched at an angle of 40 ° above horizontal on level ground at a velocity of 500 m/s, calculate the maximum height reached, the time spent in the air and the horizontal range.
g = 9.81 (m/s)/s
Firstly split the launch velocity into its vertical and horizontal components.