Normal modes: Spring and pendulum

[LCSphysicist]

Homework Statement

.

Relevant Equations

.

I was doing the exercise as follows:

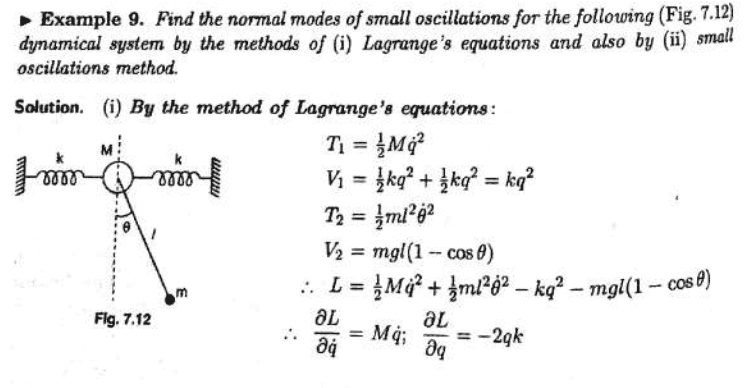
I am not sure if you agree with me, but i disagree with the solution given.
I was expecting that the kinect energy of the mass $m$ ($T_2$) should be $$T_2 = \frac{m((\dot q+lcos(\theta)\dot \theta)^2 + (lsin(\theta) \dot \theta)^2)}{2}$$
I could be wrong, of course, but i have tried to figure out my error and was not able to discover. So my guess is that the solution can be wrong.

 

[TSny]

Your expression for $T_2$ looks correct. For small oscillations it can be simplified a little.

The expression for $T_2$ in the solutions is not correct.