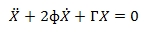Normalization and Scaling with Matrices

Click For Summary

Discussion Overview

The discussion revolves around the normalization and scaling of second order systems when the parameters involved are matrices rather than scalars. Participants explore the implications of this change on the normalization process, particularly in the context of differential equations and state space representation.

Discussion Character

  • Exploratory
  • Technical explanation
  • Debate/contested
  • Mathematical reasoning

Main Points Raised

  • One participant seeks clarification on whether the normalization steps differ when dealing with matrices instead of scalars, specifically in the context of a second order system.
  • Another participant questions the specific type of normalization being referred to, noting that it can mean different things in different contexts, such as converting to dimensionless form.
  • A participant expresses interest in producing dimensionless and scaled parameters to improve the condition number of the dynamics matrix in state space form.
  • There is uncertainty about how to nondimensionalize a system of simultaneous differential equations, with one participant explaining that the process involves substituting new variables and dividing by constants across the equations.
  • A participant mentions the potential for using linear combinations of equations in a system but is unclear about the simplification possibilities this introduces.
  • One participant shares a resource for nondimensionalizing a predator-prey system as an example, indicating the difficulty in finding relevant examples online.

Areas of Agreement / Disagreement

Participants express varying levels of understanding and agreement regarding the normalization process for matrix systems. There is no consensus on the specific steps or methods to be used, and the discussion remains unresolved regarding the best approach to take.

Contextual Notes

Participants acknowledge the complexity introduced by working with systems of equations and the challenges in finding clear examples or guidelines for nondimensionalization in this context.

doublee89
Messages
1
Reaction score
0
Hey everyone, I understand how to normalize a second order system, but I wanted to know if the same steps are taken when the parameters of the system are not scalar but matrices. For example

eq.png


where the parameter phi, and gamma are both 3x3 matrices and X is a 3x1 vector.

From what I've see online it doesn't look like it's the same when matrices are involved, and I can't seem to even find a textbook that will walk me through this step by step.

Any ideas?
 
doublee89 said:
Hey everyone, I understand how to normalize a second order system,

What kind of "normalization" are we going to do ? In some contexts, the term "normalize" means to put a differential equation into dimensionless form.
 
That is exactly the kind of normalization I was hoping for. Also, I know that in the scalar case normalizing the differential equation can reduce the number of parameters (which would also be a plus) but more than anything else I care about producing dimensionless and scaled parameters. The scaling is important to me because I will be putting this differential equation in state space form. The resulting dynamics matrix is poorly conditioned for some values and I would like to improve the condition number in the general case. This normalization/scaling could help with that.
 
SPFF said:
That is exactly the kind of normalization I was hoping for.

I'm confused. Are you working the same problem as @doublee89 ?
 
That was me (doublee89).. I am not sure why my account name has been changed. Strange...
 
Perhaps you browser saved the wrong user name and password for auto-login.

I don't know of any way to specify an algorithm to "nondimensionalize" a system of simultaneous differential equations.

Your matrix differential equation is equivalent to 3 simultaneous differential equations. The steps to "nondimensionalize" a single differential equation involve substituting a constant times a new variable for an old variable and dividing the equation by constants. Working with a system of equations, when we substitute a new variable for an old one, we can do it in all the equations. We can divide anyone of the equations by a constant.

The new possibility that a system of equations introduces is that we can replace an equation by a linear combination of other equations. It isn't clear to me whether changing variables creates any possibilities for simplifying the system of equations though using linear combinations that weren't already there in the original equations.

I agree that it's hard to find examples of nondimensionalizing a system of equations on the web. I did find this example of nondimensionalizing the two differential equations for a predator-prey system: https://daphnia.ecology.uga.edu/ceesg/wp-content/uploads/2014/01/nondim_notes.pdf
 
Last edited by a moderator:
  • Like
Likes   Reactions: jim mcnamara

Similar threads

Undergrad Empirical temperature scales using different thermometers
  • · Replies 7 ·
Replies
7
Views
3K
Graduate Relationship between Wilson's RG and the Callan-Symanzik Equation
  • · Replies 2 ·
Replies
2
Views
2K
Graduate Diagonalization of 2x2 Hermitian matrices using Wigner D-Matrix
  • · Replies 4 ·
Replies
4
Views
5K
Graduate 4th order tensor inverse and double dot product computation
  • · Replies 1 ·
Replies
1
Views
4K
Undergrad Acceleration in Newton's second law
  • · Replies 5 ·
Replies
5
Views
3K
Graduate Numerical Hartree Fock with Finite Difference Matrices for Helium
  • · Replies 4 ·
Replies
4
Views
3K
Is it possible for [A:B1] to have a unique solotion...?
  • · Replies 20 ·
Replies
20
Views
3K
Graduate About ellipticity and a proof that a system of PDEs is elliptic
  • · Replies 0 ·
Replies
0
Views
3K
Graduate C* algebras, states, finite graphs
  • · Replies 1 ·
Replies
1
Views
2K
Studying Skipping Chapters in Stewart’s Calculus? (Pearson's Edexcel IAL Background)
  • · Replies 2 ·
Replies
2
Views
936