- #1
zenterix
- 480
- 70
- TL;DR Summary
- I am reading the book "Heat and Thermodynamics" by Zemansky and Dittman. Very good book.
I have consulted many books and this book has the best discussion about thermometers and temperature scales that I have seen so far.
However, I have some questions.
It took me a while to understand (I think) the concepts below. I have two questions.
1) What does "absolute" mean in the term "absolute temperature scale"?
2) What is the difference between the two constant-volume hydrogen gas thermometers (one at high pressure the other at low pressure) displayed in the last table shown below?
To understand what I mean with these questions, I will go through the reasoning presented in the book and define a few terms (mostly by paraphrasing from the book, but also with my own interpretations mixed in).
I would really appreciate answers in the contexts presented below.
Thermodynamics directs attention to the interior of a system. Emphasis is placed on those macroscopic quantities which have bearing on the internal state of a system. Experiments are used to determine the quantities that are useful to describe such an internal state. Such quantities are called thermodynamic coordinates.
Thermal equilibrium is the state achieved by two (or more) systems, characterized by restricted values of the coordinates of the systems, after they have been in communication with each other through a diathermic wall.
An isotherm is the locus of all points representing states in which a system is in thermal equilibrium with one specific state of another system (and also in equilibrium with all other points on the isotherm itself).
Corresponding isotherms are isotherms of two different systems that represent states of thermal equilibrium between the systems.
Here is an example:
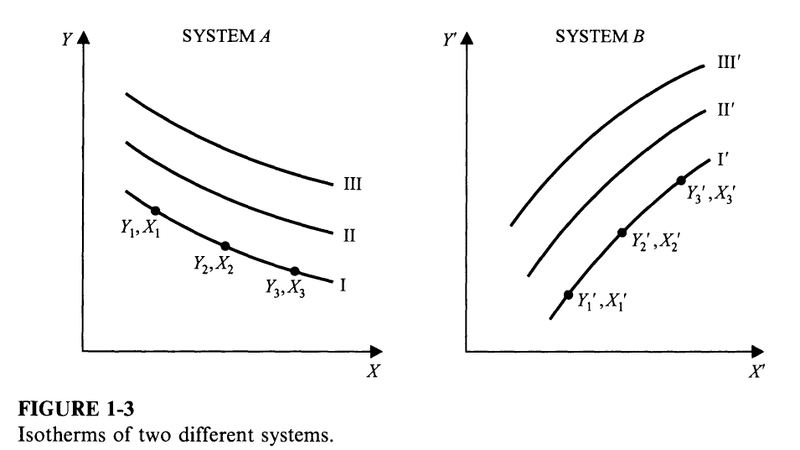
In this example, the three following states of system B, ##(Y_1', X_1')##, ##(Y_2', X_2')##, and ##(Y_3', X_3')## are all in thermal equilibrium with each other, and all are in thermal equilibrium with each of ##(Y_1, X_1)##, ##(Y_2, X_2)##, and ##(Y_3, X_3)## of system A. Indeed any point on the corresponding isotherm of system B is in thermal equilibrium with the corresponding isotherm of system A.
The temperature of a system is a property that determines whether or not a system is in thermal equilibrium with other systems.
Temperature is a scalar quantity, and so all systems in thermal equilibrium have the same temperature.
A temperature scale is a set of rules for assigning one number to a set of corresponding isotherms, and a different number to a different set of corresponding isotherms.
Once this assignment of temperatures is made, the necessary and sufficient condition for thermal equilibrium between two systems is that they have the same temperature.
A thermometer is some specific system with thermodynamic coordinates X and Y that we designate the standard system plus a set of rules for assigning a temperature to that system's isotherms. To every system in thermal equilibrium with a specified thermometer at some specific coordinates, we assign the same temperature as assigned to the thermometer's isotherm at those specific coordinates.
One way (perhaps the simplest) to make the assignment of values to the isotherms is to fix one thermodynamic coordinate (Y) and vary the other one (X). The temperature of an isotherm is then some function ##\theta(X)##.
Coordinate ##X## is called the thermometric property and ##\theta(X)## is the thermometric function.
Here is an example
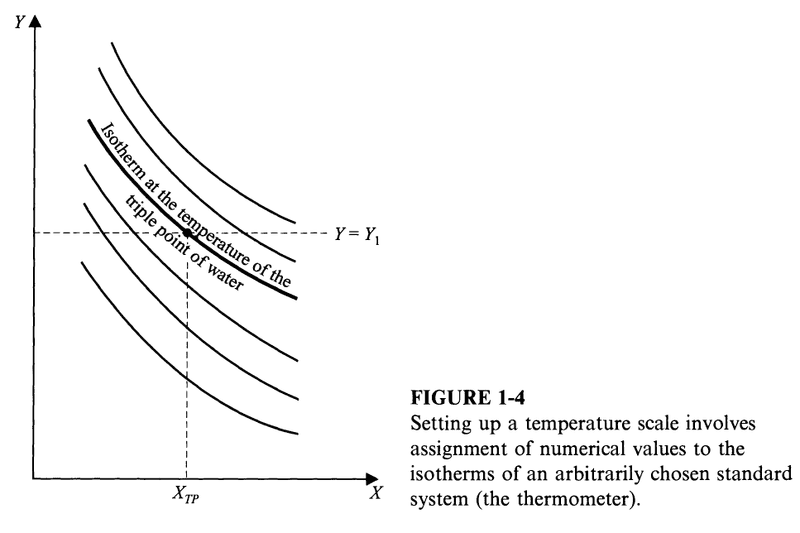
The thermometric function is also what we call an empirical temperature scale.
There are many different kinds of thermometer, each with its own thermometric property. Here is a table with six modern thermometers and their thermometric properties.

Now, let's choose one of the thermometric properties in the table above and call it X and let's define ##\theta## as a constant times X. That is ##\theta(X)=aX## where ##a## is a constant. Note that ##Y## is held constant.
My first question is about the following statement
What characteristic or quality does the word "absolute" signify in this terminology?
Note that by choosing different thermometers (that is, different specific systems to serve as a standard against which we compare other systems) we can obtain different empirical temperature scales even when we use the same thermometric function and thermometric property.
For example, we could use different gases at constant volume and specify the same thermometric properties for each resulting thermometer.
As a more specific example we could have two thermometers, one is hydrogen at a constant volume V and variable pressure P, and the other is nitrogen at same constant volume V and variable pressure P. The thermometric property is pressure in both cases.
If we then take a third system (say water at triple point), and we put each constant volume gas in contact with the third system until thermal equilibrium is established, the specific pressure at which this occurs will be different for each of the two gases we have. Yet the temperature of all three systems must be the same in this thermal equilibrium. That is, ##\theta_A(P_{A,TP})=\theta_B(P_{B,TP})=T_{TP}##.
This means that the constant ##a## will be different for each of the thermometric functions.
The next step in this whole reasoning is to choose that third system in a very specific way, ie choose a standard reference system in a specific reproducible state that we call a fixed point, ie a fixed temperature.
The fixed point is a reference temperature for the determination of temperature scales.
I now explain why this is by using a real-world example.
In 1954, a single fixed point was chosen as the basis for a new international temperature scale, the Kelvin scale. This chosen fixed point is the triple point of water.
From what I understand, there is only a single value of pressure and a single value of temperature at which the triple point occurs. The pressure is the partial vapor pressure of the gaseous water at 611.657 Pa. (This part is still not too clear for me, because I have trouble with the part about this being true regardless of the volume of water.)
However, the type of water in this reference system is also specified in detail (for example, the proportion of isotopes of hydrogen and oxygen).
So, for a system with this specific type of water at the pressure of 611.657 Pa and at triple point, the temperature was assigned a value, 273.16K.
By assigning this value we have, ##\theta(P_{TP})=273.16=aX_{TP}##.
Thus, for any thermometric property of our choosing we can measure its value at the triple point of water (for whatever thermometer we are using), and then we can solve for ##a##.
$$a=\frac{273.16}{X_{TP}}$$
Hence, for all thermometers that assign the temperature 273.16K to the triple point, we have the relationship
$$\theta(X)=273.16\frac{X}{X_{TP}}$$
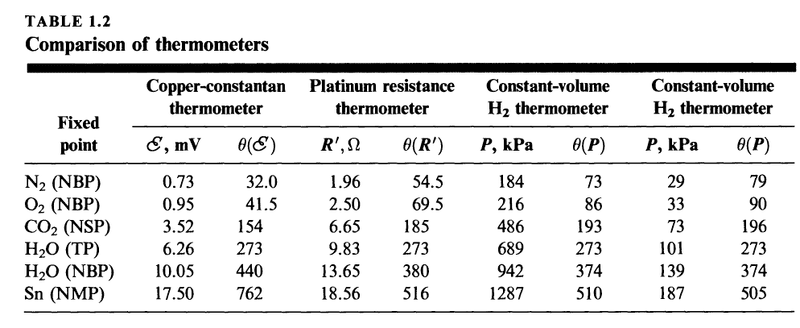
My second question is about the following table
NBP = normal boiling point
NMP = normal melting point
NSP = normal sublimation point
TP = triple point
What we have here is three different thermometers (in the columns) and six different thermodynamic states (rows). Note that in the last four columns we have the same thermometer, hydrogen gas at a specific constant volume, but used in one case at high pressure and in one case at low pressure. My doubt is about this distinction, and I'll get to this further below.
The numerical values are not meant to be exact and 273.16 has been written as 273.
Just to be clear, as an example, if we take the platinum wire resistor thermometer, which uses resistance as the thermometric property, we have
$$\theta(R')=273.16\frac{R'}{R_{TP}'}$$
My question is about the two constant-volume ##H_2## thermometers.
What does it mean that one is at high pressure and the other is at low pressure?
Here is what I think this means
If the volume of one constant-volume thermometer is larger than the other, then the pressure at the triple point will be relatively smaller, as we see in the table. In fact, at any temperature, the pressure will be smaller than the constant-volume thermometer with the smaller volume.
Is this correct?
1) What does "absolute" mean in the term "absolute temperature scale"?
2) What is the difference between the two constant-volume hydrogen gas thermometers (one at high pressure the other at low pressure) displayed in the last table shown below?
To understand what I mean with these questions, I will go through the reasoning presented in the book and define a few terms (mostly by paraphrasing from the book, but also with my own interpretations mixed in).
I would really appreciate answers in the contexts presented below.
Thermodynamics directs attention to the interior of a system. Emphasis is placed on those macroscopic quantities which have bearing on the internal state of a system. Experiments are used to determine the quantities that are useful to describe such an internal state. Such quantities are called thermodynamic coordinates.
Thermal equilibrium is the state achieved by two (or more) systems, characterized by restricted values of the coordinates of the systems, after they have been in communication with each other through a diathermic wall.
An isotherm is the locus of all points representing states in which a system is in thermal equilibrium with one specific state of another system (and also in equilibrium with all other points on the isotherm itself).
Corresponding isotherms are isotherms of two different systems that represent states of thermal equilibrium between the systems.
Here is an example:
In this example, the three following states of system B, ##(Y_1', X_1')##, ##(Y_2', X_2')##, and ##(Y_3', X_3')## are all in thermal equilibrium with each other, and all are in thermal equilibrium with each of ##(Y_1, X_1)##, ##(Y_2, X_2)##, and ##(Y_3, X_3)## of system A. Indeed any point on the corresponding isotherm of system B is in thermal equilibrium with the corresponding isotherm of system A.
The temperature of a system is a property that determines whether or not a system is in thermal equilibrium with other systems.
Temperature is a scalar quantity, and so all systems in thermal equilibrium have the same temperature.
A temperature scale is a set of rules for assigning one number to a set of corresponding isotherms, and a different number to a different set of corresponding isotherms.
Once this assignment of temperatures is made, the necessary and sufficient condition for thermal equilibrium between two systems is that they have the same temperature.
A thermometer is some specific system with thermodynamic coordinates X and Y that we designate the standard system plus a set of rules for assigning a temperature to that system's isotherms. To every system in thermal equilibrium with a specified thermometer at some specific coordinates, we assign the same temperature as assigned to the thermometer's isotherm at those specific coordinates.
One way (perhaps the simplest) to make the assignment of values to the isotherms is to fix one thermodynamic coordinate (Y) and vary the other one (X). The temperature of an isotherm is then some function ##\theta(X)##.
Coordinate ##X## is called the thermometric property and ##\theta(X)## is the thermometric function.
Here is an example
The thermometric function is also what we call an empirical temperature scale.
There are many different kinds of thermometer, each with its own thermometric property. Here is a table with six modern thermometers and their thermometric properties.
Now, let's choose one of the thermometric properties in the table above and call it X and let's define ##\theta## as a constant times X. That is ##\theta(X)=aX## where ##a## is a constant. Note that ##Y## is held constant.
My first question is about the following statement
Notice that as the coordinate X approaches zero, the temperature also approaches zero, because no arbitrary constant is added to the function. In effect, this linear function also defines an absolute temperature scale, such as the Kelvin scale or the Rankine scale.
What characteristic or quality does the word "absolute" signify in this terminology?
Note that by choosing different thermometers (that is, different specific systems to serve as a standard against which we compare other systems) we can obtain different empirical temperature scales even when we use the same thermometric function and thermometric property.
For example, we could use different gases at constant volume and specify the same thermometric properties for each resulting thermometer.
As a more specific example we could have two thermometers, one is hydrogen at a constant volume V and variable pressure P, and the other is nitrogen at same constant volume V and variable pressure P. The thermometric property is pressure in both cases.
If we then take a third system (say water at triple point), and we put each constant volume gas in contact with the third system until thermal equilibrium is established, the specific pressure at which this occurs will be different for each of the two gases we have. Yet the temperature of all three systems must be the same in this thermal equilibrium. That is, ##\theta_A(P_{A,TP})=\theta_B(P_{B,TP})=T_{TP}##.
This means that the constant ##a## will be different for each of the thermometric functions.
The next step in this whole reasoning is to choose that third system in a very specific way, ie choose a standard reference system in a specific reproducible state that we call a fixed point, ie a fixed temperature.
The fixed point is a reference temperature for the determination of temperature scales.
I now explain why this is by using a real-world example.
In 1954, a single fixed point was chosen as the basis for a new international temperature scale, the Kelvin scale. This chosen fixed point is the triple point of water.
From what I understand, there is only a single value of pressure and a single value of temperature at which the triple point occurs. The pressure is the partial vapor pressure of the gaseous water at 611.657 Pa. (This part is still not too clear for me, because I have trouble with the part about this being true regardless of the volume of water.)
However, the type of water in this reference system is also specified in detail (for example, the proportion of isotopes of hydrogen and oxygen).
So, for a system with this specific type of water at the pressure of 611.657 Pa and at triple point, the temperature was assigned a value, 273.16K.
By assigning this value we have, ##\theta(P_{TP})=273.16=aX_{TP}##.
Thus, for any thermometric property of our choosing we can measure its value at the triple point of water (for whatever thermometer we are using), and then we can solve for ##a##.
$$a=\frac{273.16}{X_{TP}}$$
Hence, for all thermometers that assign the temperature 273.16K to the triple point, we have the relationship
$$\theta(X)=273.16\frac{X}{X_{TP}}$$
My second question is about the following table
NBP = normal boiling point
NMP = normal melting point
NSP = normal sublimation point
TP = triple point
What we have here is three different thermometers (in the columns) and six different thermodynamic states (rows). Note that in the last four columns we have the same thermometer, hydrogen gas at a specific constant volume, but used in one case at high pressure and in one case at low pressure. My doubt is about this distinction, and I'll get to this further below.
The numerical values are not meant to be exact and 273.16 has been written as 273.
Just to be clear, as an example, if we take the platinum wire resistor thermometer, which uses resistance as the thermometric property, we have
$$\theta(R')=273.16\frac{R'}{R_{TP}'}$$
My question is about the two constant-volume ##H_2## thermometers.
What does it mean that one is at high pressure and the other is at low pressure?
Here is what I think this means
If the volume of one constant-volume thermometer is larger than the other, then the pressure at the triple point will be relatively smaller, as we see in the table. In fact, at any temperature, the pressure will be smaller than the constant-volume thermometer with the smaller volume.
Is this correct?
Attachments
Last edited:
