Oblique collision - quick Q - exam is tomorrow

[jsmith613]

I am capable of solving momentum problems but am looking for a way to make things easier / provide a second method as a check-point...

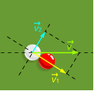
If two objects (lets assume they are of different mass as I know the problem works for objects of the same mass) collide (as in the attachment where V = initial velocity of white ball and V₁ = velocity of red ball, V₂ = final velocity of white ball)
will the white ball transfer ALL OF its velocity component that acts along the centre of masses of the ball to the red ball

Note: the situation in the attachment shows how to objects of the SAME mass collide...I don't know if it will be the same for two objects of different masses...this is what my question is about :)

Also, will the two objects move off at right angles to each other if the collision is elastic REMEMBERING masses are not the same?

 

[jsmith613]

or would I do the same diagaram but instead of using velocity, I use momentum...this seems more sensible to me...is my latter through correct?

 

[Doc Al]

Can you prove such a claim for equal masses? That should answer your question.

 

[jsmith613]

Can you prove such a claim for equal masses? That should answer your question.

Well for equal masses you know that total KE is conserved and total momentum is conserved so if you use vector dot products the two equations are only consistent if the objects move at right angles...I cannot be sure if they will move at right angles if the objects have different masses..

 

[Ken G]

In doing collisions, it is generally useful to be in the center of mass frame, and answer your questions from that perspective, after translating the question into that frame as well. In the center of mass frame, a momentum conserving collision has a simple attribute-- it looks, both before and after the collision, like two masses with opposite motions along the same line and speeds in inverse proportion to their mass, which also means that the speed of neither particle changes-- only their direction. The way the direction gets rotated between the initial and final motions depends on the angle of the collision in detailed ways that are not important for your question.

Your first question is whether or not one mass can stop and the other start. In the COM frame, that means the angle of the motion must not change-- we need a head-on collision (the frame transformation adds a constant velocity along the initial direction, so the direction cannot have a component in the other direction in the COM frame if one particle ends up stopped in the lab frame). All head-on collisions, with any masses, in the COM frame look like two particles simply reversing their velocities. The only way that could swap the particle that is stopped is if those speeds are the same, which is only when the masses are the same.

As for whether or not the collision is a right angle in the lab frame, return to the idea that the particle speeds don't change in the COM frame, regardless of mass ratio. Also, the particles end up moving away from each other. To find their angle in the lab frame, you just add the velocity of the COM to each of those opposite velocities in the COM frame. If the masses are the same, the speed you add is always half the speed that each particle has in the COM frame (which if of course the same speed). No matter what the new direction is, doing this always results in a right angle, which you can tell by taking the dot product in the lab frame and seeing that it is zero. To see the general case, just write the velocity you need to transform to the lab frame, all the particles to move off along some arbitrarily rotated direction in the COM frame, and see what happens when you take the dot product of those velocities after transforming them back to the lab frame.

 

[jsmith613]

...

Ok so to clarify what you are saying:

if we consider the collision in the COM frame, the component of momentum along COM fram (for oblique collisions) is transferred to the stationairy ball and the other ball moves at a right angle to this because we are considering velocities along COM frame. is this correct...

also if the collision we NOT elastic (i.e: inelastic) would it change the situation?

 

[jsmith613]

I realize after doing maths this is not true...the objects will only move at right angles (lab frame) if the objects have the same mass...ok problem solved