Oblique shock waves: how to find the wedge angle for trailing shock?

[Master1022]

Homework Statement

How can we find the wedge angle for the trailing shock wave?

Relevant Equations

Shock waves

Hi,

I have a question regarding oblique shockwaves.

Question: How can we determine what the wedge angle is for the shockwave in a situation?

Context: This problem here shows an oblique shock wave on the trailing edge of the body and it simply states that the wedge angle is 6 degrees. Why is this the case? Is there a general principle/method to figure these out? What if the body was completely flat on top (i.e so the body is no longer symmetric); does that change the process of knowing what the effective 'wedge angle'?

Note that the leading one makes sense to me as I can see that the flow is being turned by 6 degrees and thus that can be used in the $\theta - \beta$ relationships to find the angle of the oblique shock wave...

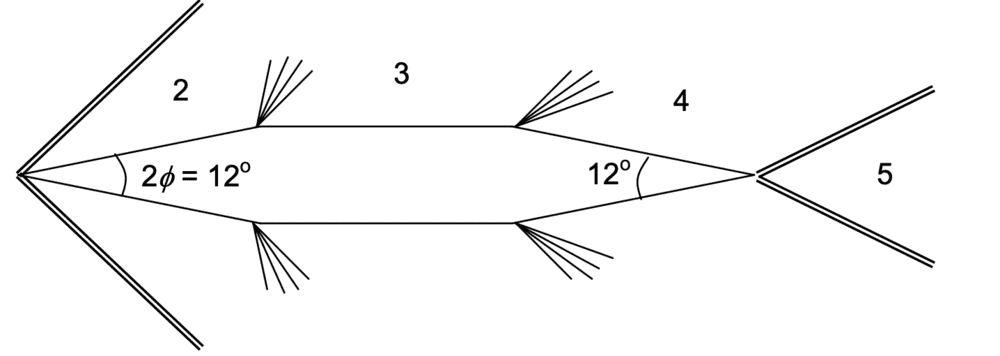
Any help would be greatly appreciated. Please let me know if this is in the wrong forum.

 

[rc1]

My understanding of supersonic / hypersonic travel is that the atmosphere acts like an incompressible liquid or solid. In aerodynamics lift is classically represented by suction on the top trailing edge of the wing this is perhaps similar to the reason for the "oblique shock wave on the trailing edge of the body". Effectively the trailing shock wave would be similar to suction or cavitation. Not sure about the mathematical version of the explanation.