Operator Language: Why d/dx*x - x*d/dx = 1

[Nezva]

When linear operators A and B act on a function ψ(x), they don't always commute. A clear example is when operator B multiplies by x, while operator A takes the derivative with respect to x. Then

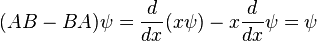
which in operator language means that

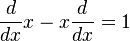
To get the last equation they divided through by ψ but why is it true? I guess what I'm trying to say is that the second equation makes no sense => d/dx*x - x*d/dx doesn't always equal 1... so why do they say that?

 

[JSuarez]

First, they don't divide it by \Psi; they simply consider it the argument of the operator AB-BA. It's akin to denote a function by f only, instead of f(x), where the variable is explicit.

Second, in this context, d/dx*x - x*d/dx doesn't always equal 1; in fact, it never equals 1: it equals the identity operator I, the one that satisfies I\Psi=\Psi.

 

[Nezva]

First, they don't divide it by \Psi; they simply consider it the argument of the operator AB-BA. It's akin to denote a function by f only, instead of f(x), where the variable is explicit.

Second, in this context, d/dx*x - x*d/dx doesn't always equal 1; in fact, it never equals 1: it equals the identity operator I, the one that satisfies I\Psi=\Psi.

Thanks for stating it so clearly and concisely. Many issues were resolved.