Optics: Center of Fizeau Fringe? Michelson Interferometer

[lechris]

Hello everyone,

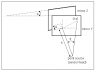
i am simulating a Michelson interferometer, where one mirror is slightly tilted, see picture.. This results in circular arcs / hyperbolic cross-section fringes. The center of these fringes depends on the focal length i am using, see picture.
Is there an analytical expression for the center of these fringes in dependency of the focal lenght?
Are there books that show the closed-form expression for such hyperbolic fringes / Fizeau fringes (so far i haven't found anything in the common literature).

Would be great if anyone has some insights on this.

Thanks!

 

[blue_leaf77]

The interference of spherical waves emitted by a pair of point sources forms a family of hyperboloids of revolution with the foci located at the two sources. Imagine a pair of point sources located at $x=-a$ and $x=a$ and further assume that the amplitudes emitted by the two source are equal, then the intensity in space at a point $(x,y,z)$ far away from either sources is given by
$$
I(x,y,z) = \frac{A}{r^2}\cos^2 \left( \frac{\pi}{\lambda}(r_2-r_1)-\frac{\Delta\phi}{2}\right)
$$
where $\Delta\phi$ is the phase lag at the sources, $r_1 = \sqrt{(x+a)^2+y^2+z^2}$, $r_2 = \sqrt{(x-a)^2+y^2+z^2}$, and $r = (r_1+r_2)/2$. You can determine the shape of the surface of constant phase difference (phase difference is simply the argument of $\cos^2$) by equating the argument of $\cos^2$ to certain value. For interference maximum, obviously this value must be $m\pi$ where $m$ is an integer. I will leave to you that the expression
$$
\frac{\pi}{\lambda}(r_2-r_1)-\frac{\Delta\phi}{2} = C
$$
with $C$ constant does form a hyperboloid of revolution, e.g. by taking square twice. Thus if you place a screen for example at the plane $z=Z$, you will observe alternating fringes in a form of hyperbolas.

 

[lechris]

Hi blue_leaf77,
thanks for your answer. The problem is, i don't have 2 spherical wave emitted by a point source. I have an extended light source with radial aperture transmitted through a positive lens, see picture original post. I still don't see how the center of the interference fringes relates to the focal length of the length.
The closest i came to the solution is what i have attached as a drawing, but it still does not address the problem of an extended light source with positive lens.

 

[blue_leaf77]

How does the beam from your extended source come to the lens? Will it approximate your application if the beam is modeled by a Gaussian beam? If yes, the focal point behind the lens can be well approximated by a point source. If not, then it might be too complicated to give a closed form equation.

Are there books that show the closed-form expression for such hyperbolic fringes / Fizeau fringes (so far i haven't found anything in the common literature).

That's what you asked. The equation in post#2 addresses the indirect answer to this question. You can also find a similar expression in "Optics" by Bruno Rossi. But he also treated the case of a pair of point sources.

 

[lechris]

How does the beam from your extended source come to the lens? Will it approximate your application if the beam is modeled by a Gaussian beam? If yes, the focal point behind the lens can be well approximated by a point source. If not, then it might be too complicated to give a closed form equation.

I use a simulation software which initializes an optical field and i instantly create the lens afterwards, so the optical field source and the lens are on top of each other. The software uses Fourier optics for the simulation. All i specify is the focal length, wave length and aperture size.
My primary goal is to find the center of the fringes that appear on the screen (with respect to the mirror angle). A closed-form solution of the fringes would be great but the fringe center would suffice. I just thought it is necessary to have a closed-form solution to derive the center point.
I have attached an equivalent drawing of the Michelson setup. Shouldn't it be possible to find the center of fringes solely using ray optics (virtual screens M1' and M2' need to be overlaid)? For solving the problem with a Gaussian beam i would need the initial waist size of the beam, which i don't have unfortunately.