Optics (refraction) question

[dalcde]

Homework Statement

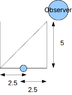
The length of each side of an opaque cubic container is 5 cm and a coin is placed at the center of the base as shown. At this instant, the observer is unable to see the coin. However, the coin can just be seen when the container is fully filled with liquid A. Find the refractive index of liquid A. (You may regard the coin as a point)

Homework Equations

Snell's Law
$$n_1\sin\theta_1=n_2\sin\theta_2$$

The Attempt at a Solution

I assumed that the apparent position of the coin is on the diagonal line, which means when the ray is refracted at the top-right corner, the refracted angle will be 45 degrees. Hence
$$n\sin\tan^{-1}\frac{1}{2}=\sin\frac{\pi}{2}$$
and
$$n=1.58$$
However, the solution give is 2.24 (it would be a rather unusual refractive index for a liquid), which is (I think) calculated by assuming that the apparent position of the coin is on the surface of the liquid. Which assumption is correct and why?

Thanks in advance

P.S. why aren't we allowed to attach svg images?

 

[Delphi51]

That's a very confusing diagram! I drew

The red line shows the ray from the coin to the eye, bending at the surface of the liquid. You can calculate A1 and A2 using trigonometry. Then use Snell's law to get the index of refraction. Oh - you got it right already, 1.58. Sorry, I didn't understand your one-line solution at first!

There is no way the image can appear at the surface.

The forum must have had trouble with inappropriate images. It works perfectly if you upload your image to a service like photobucket.com, get its IMG link and paste in your post. That's what I did.

 

[dalcde]

Thanks.

By the way, the image is fine. It's just that I was rather sleepy when drawing it and didn't bother to draw much (and what I draw was exactly what was drawn on the question)

 

[rl.bhat]

In the problem, it is not mentioned that the observer is seeing the edge of the cubic cotainer. So he can see the object when it is in the line of sight. When the eye is slightly off the line of sight, the object cannot be seen. So you have to assume that the eye sight is along the surface of the container. In this position he can see the object, if the angle of incidence is the critical angle.

 

[Delphi51]

rl.bhat, I don't understand that! I would appreciate a longer explanation if you aren't too busy today. For one thing, it seems to me that if the ray hits the water surface at the critical angle, it will not escape the liquid and therefore will not be seen at all.

I now see that the OP created the diagram from the question and there is no good justification for the assumption that the eye is in the location shown.

 

[rl.bhat]

Hi Delphi51, since the observer is not seeing the object, his eye is away from the line joining the coin and the top edge of the container. As he pours the liquid, the angle of incidence goes on decreasing. If the light refracts, it will hit the wall of the container. If the angle of incidence is greater than the critical angle, he will not see the object at all til the container is full of liquid. If the angle at the top edge is the critical angle, the ray will come out horizontally and the observer can see the object.

 

[Delphi51]

A very interesting interpretation of the vague question!
So Snell's Law is sin(45)/sin(90) = 1/n --> n = 1.41.
OP says the answer is supposed to be 2.24.

It seems to me the eye is just on the edge of seeing a ray from the coin going past the top edge of the container, so any liquid with n > 1 will refract the ray slightly and make the coin visible.

 

[rl.bhat]

The angle of incidence at the top corner is not 45 degrees. sin(C) = sqrt(1/5)
So the refractive index n = sqrt(5) = 2.24

 

[Delphi51]

Oops, that was dumb! I looked at the wrong diagram. Thank you.